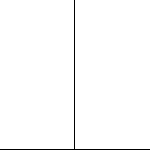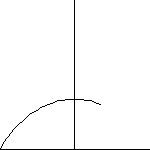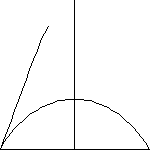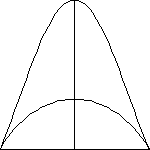| Back to . . . |
 Baseball |
 Mark McGwire |
Measuring Home Run Distance
|
On
May 22, 1963,
Mickey Mantle, the great New York Yankee slugger, hit a prodigious home
run; some say the longest ball ever hit in the major leagues. Although
it struck the stadium roof only 370 feet from home plate, some news
reports
credited Mantle with a 620-foot blast. Why was there this vast
discrepancy?
By tradition, when a batter hits a home run and it lands somewhere
within
the ball park, the distance this home run is said to have traveled is not
the distance to the point of impact, but the estimated distance the
ball would
have traveled had its flight been unobstructed. As we shall see, in
Mantle's case, this distance may have been considerably exaggerated.
|
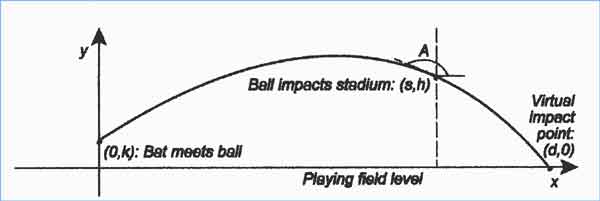
|
1.
The ball’s
height above the field at the point of impact with the stadium ( h
in the diagram).
2.
The horizontal
distance that the ball has traveled when it impacts the stadium ( s
in the diagram).
3.
The angle
of impact — the angle that the tangent line to the flight path makes
with
the horizontal
( A in the diagram).
4.
The height
at which the bat struck the ball (k in the diagram).
|
|
To
calculate
the distance, we view the parameters h, s, A, and k as
given
and assume that the path of the batted ball is a parabola, at least
from
the point of impact with the stadium to the “virtual impact point” with
the ground — the spot at which the ball would have hit the ground had
its
path been unobstructed. Traditionally, these parameters have been
estimated
with the aid of a tape measure and careful observation of the ball’s
flight
path. Today, sophisticated technology (see, for example, reference [4])
can provide much more accurate figures for these variables.
|
The Calculation
|
(1) When x = 0, y
= k.
(2) When x = s, y = h. (3) When x = s, dy/dx = tanA.
Condition (1) yields c
= k.
Conditions (2) and (3) result in the linear system (with unknowns a
and b):
tan(A) = 2 as + b Solving this system, we see that a = [ s(tanA) - h + k] / s2 and b = [2h - s(tanA) - 2 k] / s . Once a and b have been calculated, the home run distance, d , is determined by finding the positive solution of the quadratic equation ax2 + bx + k = 0.. As an example, suppose a batter hits a home run into the seats. A chart supplied by the home club tells us that the ball landed 50 feet above the playing field and 400 feet from home plate. Thus, h = 50and s = 400.We estimate that the bat met the ball 3 feet (k) above home plate and that the angle of impact with the stadium was 135 E ( A). Then, using the formulas given above, we see that the path of the ball has the equation y = ax2 + bx + c, where a = -0.00279, b = 1.235, and c = 3. So, the home run distance, d, is the positive solution of the equation (-0.00279)x2 + (1.235)x + 3 = 0. Using the quadratic formula, we see that d is approximately 445 feet. (Note that the actual (straight line) distance that the ball traveled to the point of impact, obtained from s and h by using the Pythagorean Theorem, is approximately 403 feet.) Note: Please see references
[2] and [5], p.
594, for other approaches to this problem.
|
|
Let’s now return to the Mantle home run that was mentioned at the top of this page. Its point of impact with the stadium was approximately 115 feet above field level (h in the formula) and 370 feet from home plate (s ). The 620-foot estimate for this blast was based on the belief that the ball was near the peak of its travel at the point of impact with the stadium, which has since been deemed to be highly unlikely (see references [1], pp. 104 - 105 and [3]). Suppose we take the more conservative view that the path of the ball made an angle of 150 E ( A in the formula) with the horizontal when it struck the stadium. We will also assume, for the sake of simplicity, that Mantle “golfed” the pitch off the ground, so that k can be taken to be 0. (This simplification alters the computed home run distance by less than a foot.) From this data, we compute the parabolic path of the ball to be y = ax 2 + bx,where a = -0.00239and b = 1.199.So, the home run distance, d, is the positive solution of the equation which is approximately 502 feet. |
cover
is formed by folding two identical perpendicular plane regions, or "curves," to form a sphere. Its circumference is 9 1/8 inches, a length that permits a pitcher to get a firm grip on the seams.
The cover was invented by a young boy, Elias Drake, in the 1840s.
|
|
| [1]
W. Adair, Robert, The Physics of Baseball (3rd
ed.), Harper and Collins, 2002.
[2]
HowStuffWorks, Question of the Day, [3] W.
Jenkinson, Long Distance Home Runs, 1996. [4]
Sportvision, HR Distance, 2002. [5] Varberg, Pursell, and Rigdon, Calculus (8th ed.), Prentice Hall, 2000. |
 |
Summer, 2002 |