The
Curve of Clavería (COC)
La Historia
Bueno,
empecemos con la curva, y para ello haremos un poco de historia. Hace
muchos años yo trabajaba en un taller de calderería
en el que se fabricaban cuerpos metálicos 3D (tolvas,
bifurcaciones, cilindros, conos, prismas, pirámides, etc)
partiendo de chapas metálicas planas (sheet metal). Había
un cuerpo que me atrajo su atención por su simplicidad y
dificultad de desarrollarlo en el plano: EL CONO OBLICUO (when the vertex of a cone is not aligned directly
above the center of its base) see figures 1

figure 1. Oblique cone
La Curva
La técnicas habituales para desarrollar el cono
oblicuo en el plano se basan en procedimientos gráficos
aproximados, tal como nos enseña la geometría
descriptiva. En la web
podemos
ver un ejemplo de un procedimiento gráfico.
Bien,
pero
la pregunta que me hice era: si la directriz del cono es una
circunferencia de radio r y cortamos el cono por una generatriz
desarrollándolo en el plano ¿cual es esa nueva curva?
¡mi curva!, que he llamado Curve of
Clavería (COC). Su conocimiento analítico nos
permitiría hacer una desarrollo del cono mucho más
preciso.
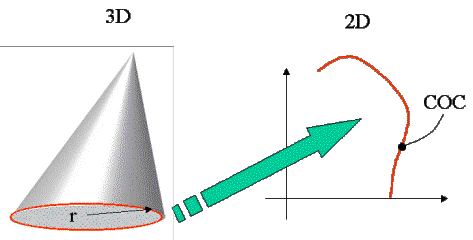
figure 2. Definition de la
Curve of Claveria (COC)
Las Propiedades
La
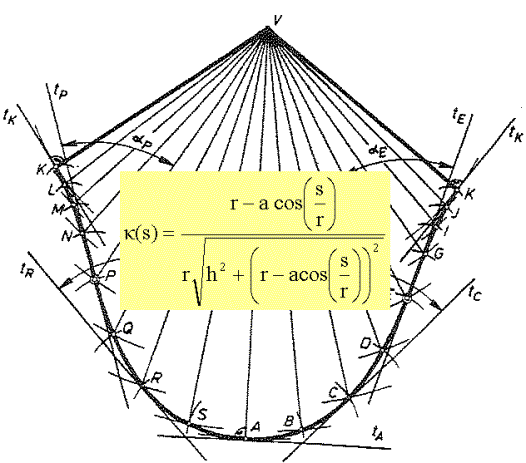
forma de la COC ya es conocida por la geometría descriptiva,
figura 3, pero ¿cual es su ecuación?
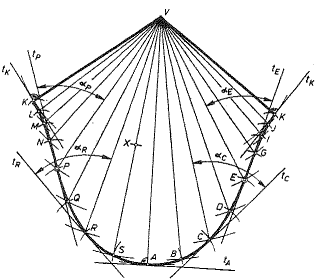
figure 3. Curve of Claveria
(COC)
Observando la figura 3 podemos ver las
siguientes características de la curva:
- es simétrica
- existen dos puntos de
inflexión (P, E)
- existen tres puntos en los cuales el
radio vector de la curva es perpendicular a su recta tangente (K, A)
Además, cuando el cono es recto
sabemos por geometría elemental que la curva COC es muy
sencilla: arco de circunferencia, fig. 4
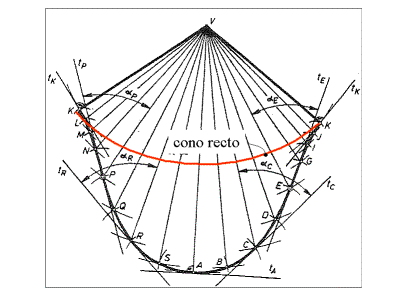
figure 4. Curve of Claveria
(COC). Right cone
La Ecuación
Para
determinar la ecuación de la COC tendremos en cuenta que en las
superficies desarrollables (conos, cilindros, superficies tangenciales)
se conserva constante la longitud de una curva perteneciente a ella
cuando la superficie la desarrollamos en el plano, luego ya sabemos la
longitud de COC : 2pr
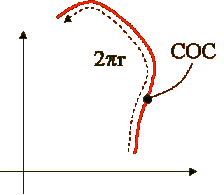
figure 5. Longitud
de la COC
Coordenadas polares parametricas
Para seguir avanzando en el conocimiento de la COC
determinaremos su radio vector y su ángulo polar. Para esto
consideramos como parámetro de la curva el ángulo t:
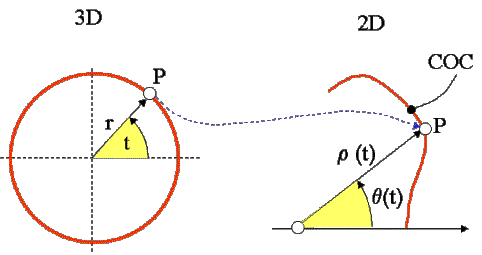
figure 6.
Coordenadas polares parametricas de la COC
1. Radio vector, r(t)
Será la distancia entre el
vértice del cono y un punto de su generatriz
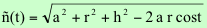 (1)
(1)

figure 7.
Generatriz del cono oblicuo vs radio vector de la COC
2. Angulo polar, q(t)
Consideraremos un trozo pequeño (diferencial) de
nuestra curva en 3D y 2D, resultando, ver figura 8
ds = r
dt
3D
ds2 = dr2 + (rdq)2
2D
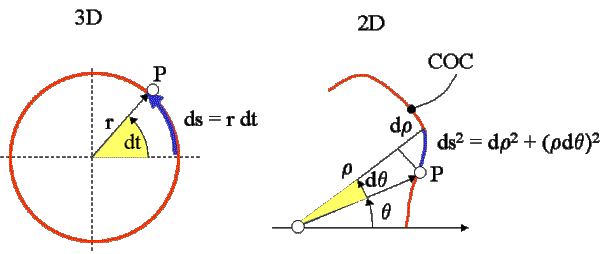
figure 8. Angulo
polar de la COC
luego,
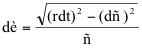
sustituyendo el valor r e integrando,
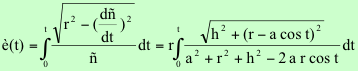 (2)
(2)
desgraciadamente
este integral es elíptica y no se
puede resolver en términos de funciones elementales.
Las
ecuaciones (1) y (2) constituyen la formulación de COC en
coordenadas polares parametricas. En coordenadas parametricas
cartesianas tendríamos
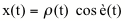 (3)
(3)
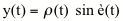 (4)
(4)
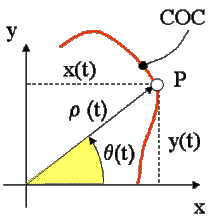
figure 9.
Coordenadas cartesianas parametricas de la COC
Ecuación intrínseca
Las ecuaciones (1) y (2) resuelven el problema planteado,
pero matemáticamente no terminan de ser “bonitas” al tener que depender de una integral “no integrable”.
Otra alternativa para formular la ecuación de la COC seria
definirla independientemente de una sistema de coordenadas: su
ecuación intrínseca. En esta formulación
relacionaremos la curvatura (k) en un punto de la curva y la longitud de la curva (s): k = k(s)
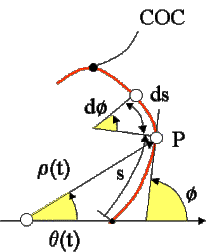
figure 10.
Definición de la ecuación intrínseca de la COC
siendo
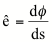
The curvature of a curve given by a polar equation r = r(q) is
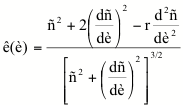 (5)
(5)
como en nuestro caso r = r(t) y q = q(t)
tendremos
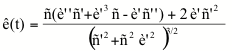 (6)
(6)
y sustituyendo las ecuaciones (1) y (2)
en (6) y teniendo en cuenta que s = r t tendremos
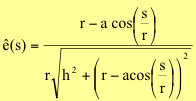 ¡Conseguido! It’s
beautiful for me
¡Conseguido! It’s
beautiful for me
s = 0 to 2 p
r
t = 0 to 2 p
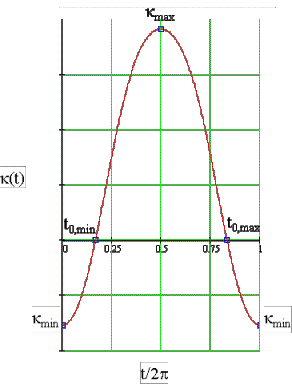
curvatura
mínima y máxima:
kmin
= k(0) = k(2pr) = 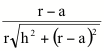 kmax
= k(pr) =
kmax
= k(pr) = 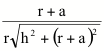
curvatura
nula (punto de inflexión):
El valor
curvatura nula se definirá para el valor de t que cumple k(t)= 0, resulta
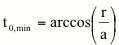 k(t0,min)
=
0
k(t0,min)
=
0
y por
simetría
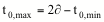 k(t0,max) = 0
k(t0,max) = 0
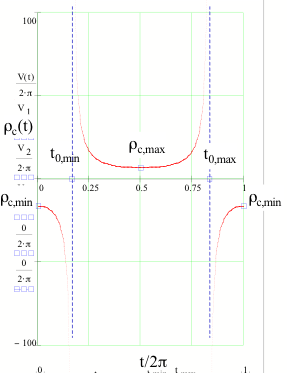
El radio de curvatura
es la
función inversa de la curvatura:
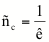
radio de
curvatura mínimo y máximo:
rc,min
= k(0) = k(2pr) = 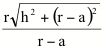 rc,max
= k(p r) =
rc,max
= k(p r) = 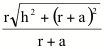
radio de
curvatura infinito (punto de inflexión):
El valor
curvatura infinito se definirá para el valor de t que cumple k(t)= 0, resulta
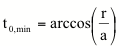 k(t0,min)
=
0
k(t0,min)
=
0
y por
simetría
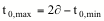 k(t0,max) = 0
k(t0,max) = 0
The
Curve of Clavería (COC)