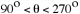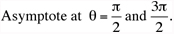| Back to . . .
Deposit #61 |
 The Conchoid Family of Curves |
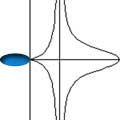 Area of the loop . . . |
|
For
the Conchoid
of Nicomedes....
 |
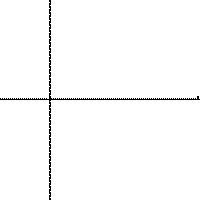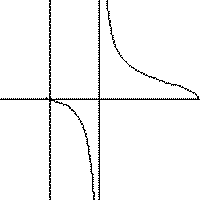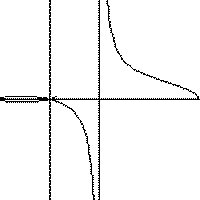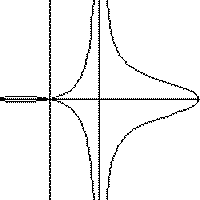
Replay the animation |
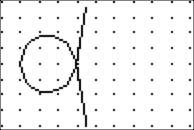
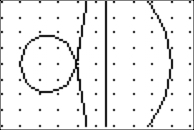
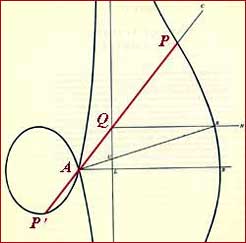
Definition: Let S be any curve and let A
be a fixed point. If a straight line is drawn through A to meet
the
curve at Q, and if P and P' are points on this line such that PQ = P'Q
=
a constant term, the locus of the points P and P' is called a conchoid
of
the curve with respect to the fixed point A.
|
|
MATHEMATICA®Code
 The Conchoid family of curves is easily entered and modified on a graphing calculator. Be sure to use (1/cos) for the secant term. |
|
Historical Sketch Nicomedes (ca. 225 BC) is credited with being the first
to investigate the conchoid, a name from the Greek meaning
"shell-like" or "shell form." He sought to find two mean
proportions between
given lengths in order to solve the famous Delian problem. The Delian problem is also known as duplication of the
cube;
in other words, finding the edge of a cube having a volume exactly
twice
that of a given cube. This is one of the three famous
constructions
dating from antiquity. If, contrary to Euclidean assumptions, we
permit ourselves to mark a straight edge, the conchoid may, in fact be
applied to these famous problems. With adjustments in various constant terms, the conchoid
is modified into a circle, spiral, limaçon, or cardiod.
Moreover, we find equations for the conchleoid and conchal as
well as focal conchoids of conic sections in the literature. But
the most famous are the . . . . . .
To underscore the historical importance of the conchoid,
we have selected Figure #139 of John Colson's translation of Maria
Gaetana Agnesi's Instituzioni analitche, now generally
recognized as the first book of mathematics written by a woman.
Colson held the prestigious Lucasian chair at
Cambridge. In 1801 he chose to translate Agnesi's widely
acclaimed treatise on Calculus written one-half century earlier (1748).
Unfortunately, his translation of the name of the curve now known in
English speaking countries as the Witch of Agnesi was a
slight, but lasting error. However, his Conchoid of Nicomedes
was accurate and an indication of the enduring fame of this popular
curve. Colson's EXAMPLE IV speaks for itself.  Reproduced with
permission from the Rare Books Division, Dept. of Rare Books and
Special
Collections, Princeton University Library.
Please observe that
Agnesi first sketched a circle to generate both her Witch and the conchoid before proceeding to give
a proof.
|
||||||||||
|
|
|||
| http://www-history.mcs.st-and.ac.uk/history/Curves/Conchoid.html | |||
| http://mathworld.wolfram.com/ConchoidCurve.html | |||
| Eves, Howard, An Introduction
to the History of Mathematics, 6th ed,. The Saunders College
Publishing, 1990. |
|||
| Gray, Alfred, Modern Differential Geometry of Curves and Surfaces with MATHEMATICA®, 2nd ed., CRC Press, 1998, p. 898. | |||
| Lockwood, E. H., A Book of
Curves, Cambridge University Press, 1961. |
|||
| Shikin, Eugene V., Handbook
and Atlas of Curves, CRC Press, 1995. |
|||
| Yates, Robert, CURVES AND
THEIR PROPERTIES, The National Council of Teachers of Mathematics,
1952. |
|||
|