Gnomon is an Island

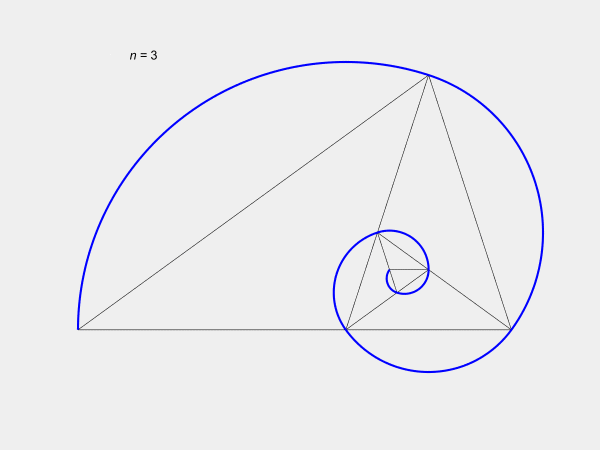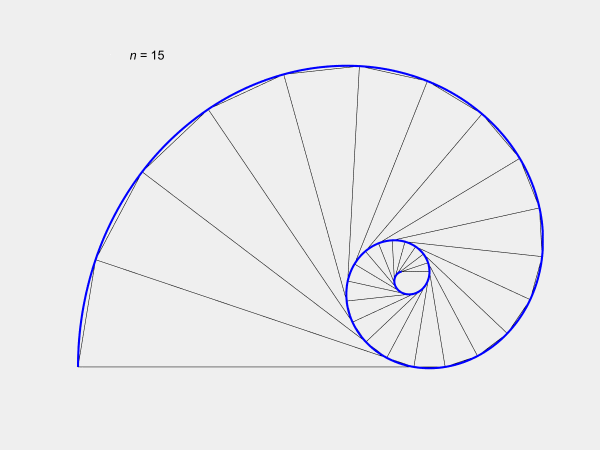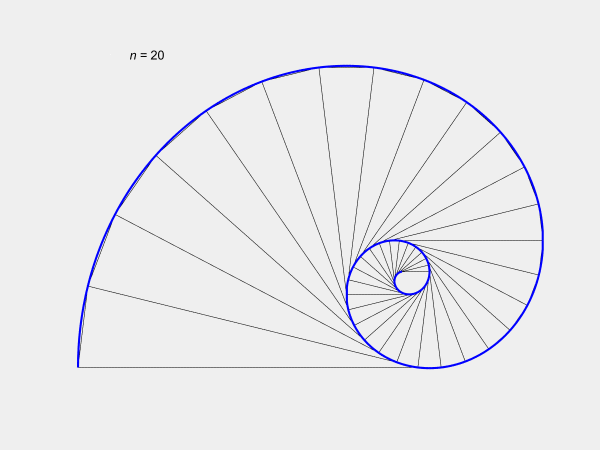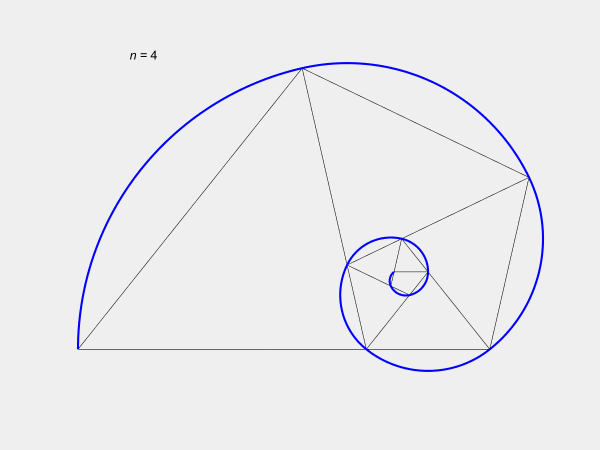
We are familiar with the concept of gnomonic tiling in which a figure added to another reproduces the shape of the original. The process can repeated over and over to form a tessellated mosaic that covers the plane. The initial tile is called the seed and the added piece is called the gnomon. The gnomon generally increases in size geometrically, i.e., by a power law. Figures thus created are called whorled figures, as the gnomons are usually added in a circular fashion about the seed. See, for example, Gazalé [1] and Waldman [2].

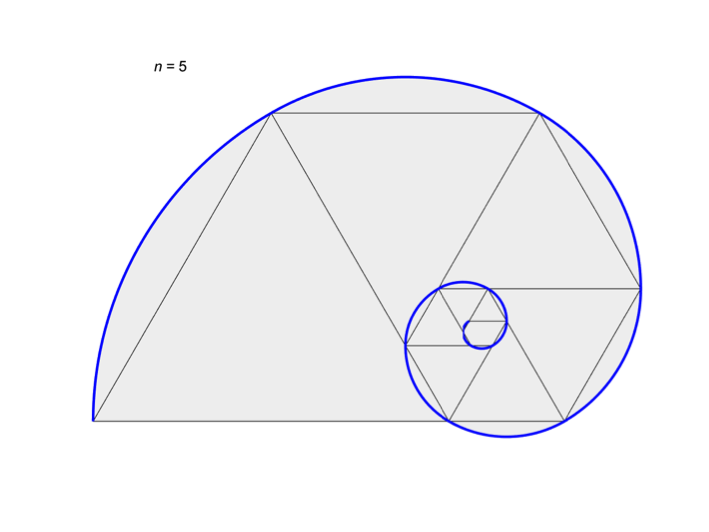
Our Figure 1 shows a whorled plastic pentagon.

There are magnificent mosaics, or tilings, if you prefer, that continue to amaze us. These are the whorled plastic pentagon, with its equilateral triangle gnomon, and the whorled golden rectangle, with its square gnomon, shown in Figure 1 and Figure 2, respectively. The former has a growth rate of p, the plastic number, and the later has a growth rate of , the golden ratio.

Figure 2: Golden rectangle and its square gnomon with a growth rate of the Golden Ratio.

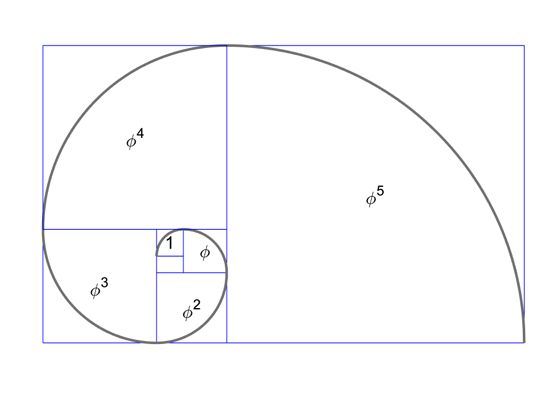
It’s fairly well established that the whorled figures in Figure 1 and Figure 2 are the only ones whose gnomons are regular polygons, by which we mean, of uniform sides and internal angles. Insofar as we have developed a program for creating pseudospirals and their attendant triangles (or squares), we wondered if we could find additional mosaics that covered the plane. . . . . . . . . . . . . . .

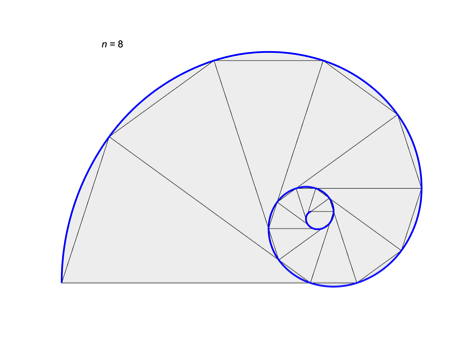Figure 3: An octagon and its golden triangle gnomon.

Voilà! We found by experimentation the pseudospirals with a sequence and rotation angle produce a whorled octagon with an isosceles triangle gnomon. The growth rate q was determined empirically. The result is shown in Figure 3. Interestingly, the gnomon is the golden triangle.

This set the stage for us to (a) determine the growth rate analytically, and (b) see if the result could be generalized for other growth rate and turn angles. The technical details and nomenclature that followed are included in the attached pdf file.