| Back to . . . .
 Curve Bank Home Curve Bank Home
 Curve Bank Index Curve Bank Index
NCB
Deposit # 103
Janet Beery
University of Redlands
Lou
Talman
Metropolitan State
Univ.
Denver
|

The Cannonball Curves of Thomas Harriot
Projectile Motion circa
1600
|
 Thomas
Harriot
Thomas
Harriot
1560-1621 |
The
English mathematician Thomas Harriot is best known for accomplishments
in three areas.
* Navigation
|
* Astronomy
|
* Algebra
|
We
now investigate his models of projectile motion; specifically,
determining the path of a cannon or mortar shot.
|
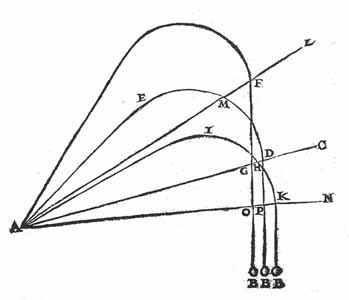
Harriot’s
first model (above) predicted the paths traced in red for shots fired
at elevation angles of 30, 45, and 60 degrees. Each of these
paths has the same maximum height and, as the elevation angle
decreases, the range increases. Harriot’s final model, predicting
the curves traced in blue, was much more realistic. This model
matches both reality and the curves predicted by classical mechanics
very well.
Harriot's
patron, Sir Walter Raleigh, sent Harriot on a voyage to the New World
in 1585. Harriot lived in what is now North Carolina for one year
before sailing back to England with Sir Francis Drake in 1586. He
wrote a book about his experiences called "A Briefe and True Report of
the New Found Land of Virginia" that was translated into many languages.
Beginning
in July of 1609, Harriot made drawings of the moon, as observed through
his brand-new telescope. This was five months before Galileo
would do the same and gain much greater recognition for it.
|
|
Earlier contributions from
Tartaglia's "Nova scientia . . ." (1537):
|
Harriot on
Projectile Motion: The Cannon Shot
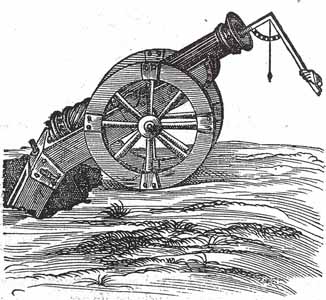
Harriot's starting point was the medieval
belief, presented in the gunnery manuals of his time, that the flight
of the cannonball began with "violent motion" out of the muzzle of the
gun and ended with "natural motion" as it fell to the ground.
Anyone who had seen a cannon or mortar shot knew that the motion did
not abruptly change from one to the other, but rather made a more
gradual transition from "violent" to "natural" motion during a period
of "mixed" motion.
Harriot would construct cannonball curves by plotting points marking
the cannonball's position in the air after equal intervals of time, and
then drawing a smooth curve connecting the points. By taking into
account both motion in the direction of the shot and motion straight
downwards due to gravity, he would combine "violent" and "natural"
motion into smooth curves.
|
|
How realistic are Harriot's First
Models?
Study
the above curves. The shape for a shot at an elevation angle of
30 to 60 degrees is fairly realistic. However, you can see
already that all trajectories seem to have the same height and that the
range of the shot increases as the elevation angle decreases.
|
Harriot's Final Models |
| * Motion
in the direction of the shot decelerates according to the sequence 15,
13, 11, 9, 7, 5, 3, 1 |
* Vertical
motion accelerates downward according to the sequence 1, 3, 5, 7, 9,
11, 13, 15
|
Angle of 30
degrees
|
Angle of 45
degrees
|
Angle
of 60 degrees
|
|
 2010
2010