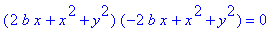| Back to . .
.
NCB
Deposit # 12
|

The Hippopede of Proclus Dr. Adam Coffman Department of Mathematical SciencesIndiana University - Purdue University Fort Wayne http://users.ipfw.edu/CoffmanA/pov/spiric.html |

|
|
|
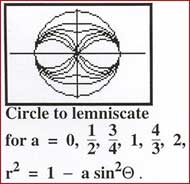
1. The
implicit equation in
the xy-plane is
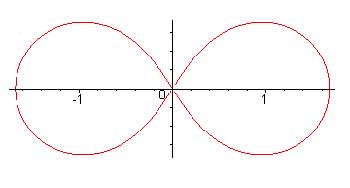
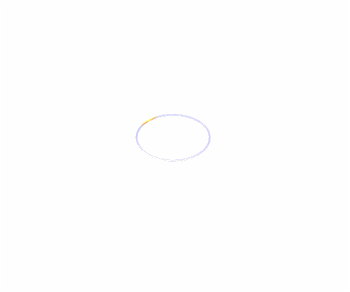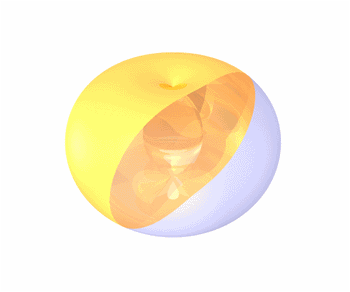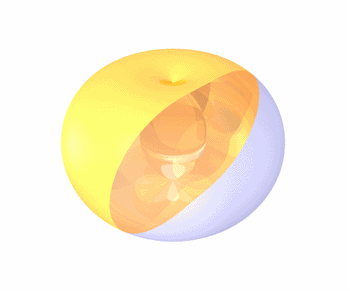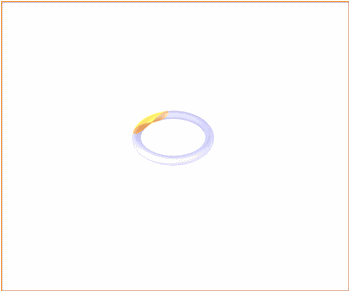
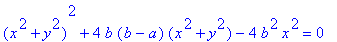 2. Any Hippopede is the intersection of a torus with one of its tangent planes that is parallel to its axis of rotational symmetry, as demonstrated in the animation. 3. Converting the implicit equation to polar coordinates gives 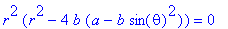 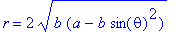 . .4. If 0 < b< a,
the point
at the origin is an isolated node and the balance of the solution set
is
a simple closed curve, also called an Elliptic Lemniscate
of
Booth. 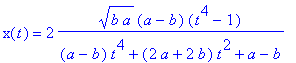 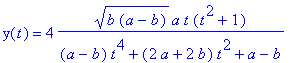 Each of these curves is the image of an ellipse under an inversion in a circle. The circle and the ellipse must have the same center. The curve is non-convex for b < a < 2b, and convex for a > 2b when the shape is oval, but is not exactly a strictly defined ellipse. 5. If a = b, the quartic implicit equation factors into two quadratics; thus, the curve is the union of two circles, centered at ( - b,0 ) and ( b, 0 ), each of radius b, and mutually tangent at the origin.
6. If 0 < a < b, the curve intersects itself at the origin, and it is also called a Hyperbolic Lemniscate of Booth.This is given by the rational parametrization 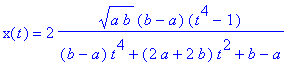 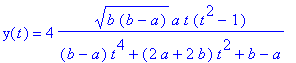
Each of these curves is the image of a hyperbola under an inversion in a circle. The circle and the hyperbola must have the same center. |
 Now that you have
investigated the equations and read of the special properites, we
suggest you use the "Reload" or "Refresh" button at the top of your
computer. This will replay the animation. Visually "slice"
the torus to see the plane lemniscate evolve into a pair of circles,
and then the oval shape.
and
|
 |
Proclus (410 - 485 A.D. ) was a
Greek mathematician
who is best known for his Commentaries on the First Book of
Euclid's
Elements. This monumental work is often our only historical
source
on ancient Greek mathematics dating from Thales to Euclid.
Though educated in Alexandria, he spent most of his highly productive life as head of the Academy of Plato in Athens. In the tradition of his time, Proclus was buried near his teacher and mentor, and not with his family. The modern student should realize the notation and graphing we use today were unknown to Proclus. Still, curiosity led to investigation of highly sophisticated curves. |

|
|
| For other animations from Coffman, see < http://users.ipfw.edu/CoffmanA/pov/spiric.html > Coffman used Maple for the calculations and the raytracer Persistence of Vision, or PoV for short, to generate the graphics. For more on Proclus, a.k.a. Booth curves, see < http://perso.club-internet.fr/rferreol/encyclopedie/courbes2d/booth/booth.shtml >. For the Hippopede of Eudoxus, see < http://mathcurve.com/courbes3d/hippopede/hippopede.shtml >. Lawrence, J. D., A CATALOG OF SPECIAL PLANE CURVES, Dover Publications, 1972. See pp.144-146. Shikin, Eugene V., Handbook and Atlas of Curves, CRC Press, 1995. ____________________
|