| Back to . . .
 Curve Bank Home
Deposit #75
A Streaming Video
|
Understanding
Infinite Series in the Calculus
Professor Michael
Krebs
Jeffrey L.
Derbidge of CSULA |
|
Harmonic
Series
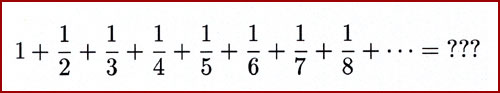
Click
here or on the picture to view their video.
Turn on your audio and be patient. The speed of your internet
connection makes a difference.
Note: This video may have problems streaming in RealOne Player.
Windows Media Player version 8 or greater is recommended. If not
installed on your computer a free
download is available.
|
Click on each image to
reveiw the steps for determing the Harmonic Series is divergent:
|
In the harmonic series, the sum of
each group of fractions being added is greater than one-half. Thus, the
harmonic series is constantly adding terms greater than any assignable
limit. We say the harmonic series diverges.
~~~~~
Convergence
occurs only if the various sums "taken, from the first, in whatever
number one wishes, finish by constantly have an absolute value less
than any assignable limit."
Cours
d'analyse de l'Ecole Royale Polytechnique, VI, Augustin-Louis
Cauchy
[From
Cauchy's lecture notes.]
~~~~~
But as always in mathematics, be
careful. The alternating
harmonic series converges.
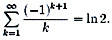This is a
result of the Taylor series of the natural logarithm.
|
|
Useful
Links and Books
|
| James Stewart, Calculus, 5th ed,.
Thomson Brooks/Cole, 2003, p. 753-754. |
| Howard Eves, An Introduction to
the History of Mathematics, 6th ed,. The Saunders College
Publishing, 1990, p. 264. |
| Victor J.
Katz, A Brief History
of Mathematics, BRIEF VERSION, Pearson
Addison
Wesley, 2004, pp. 208-210. |
Eric
W. Weisstein,
"Series" in CRC Concise Encyclopedia of MATHEMATICS,
CRC Press, 1998, p. 800 and p. 1618.
We also
recommend reading the article "Book Stacking Problem." p. 155.
Professors have illustrated the harmonic series using stacks of
books. |
|
|
Harmonic Series
James Lesko, Sums of Harmonic-Type Series,
The College Mathematics Journal, Vol.35,
No.3, May 2004, pp. 171-182.
Curtis Feist and Ramin Naimi, Almost
Alternating Harmonic Series, The College Mathematics
Journal, Vol.35, No.3, May 2004, pp. 183-191. |
Full Proofs
K. Knopp, Theory and
Application of Infinite Series, Hafner, 1951. |
|
|
|
Both the Harmonic Series and the
harmonica are named for a property of sound studied by the ancient
Pythagoreans. Given a vibrating string of length one unit,
a string of 1/2 the length will vibrate with a frequency of twice the
basic
unit. Similarly a length of 1/3 will vibrate with a frequency of
three
times the fundamental unit and so on. The combination of
frequencies produces musical harmony; thus the name.
|
|
|
Information Technology Services,
Taping and Editing by
William
Stellmacher
Dennis Kimura
Wing T. (Sterling)
Wong
|
|
|
|
