| Back to . . . | 
Lissajous or Bowditch Curves |
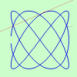
|
|
Parametric
Equations
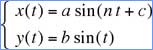
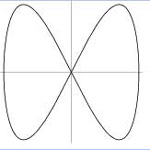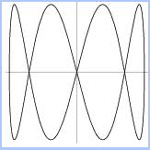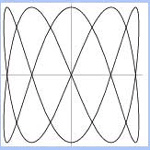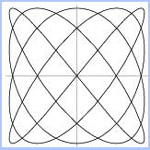
Note: The n determines the number of complete loops. The Slide Show on the right illustrates different values for the constant terms. |
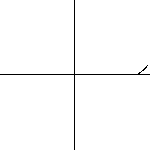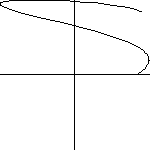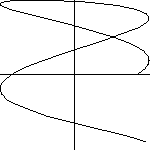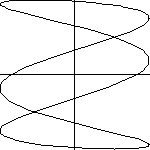
Replay the animation |
|
|
MATHEMATICA®Code

Also, these curves are easily entered and modified on a graphing calculator. |
American Nathaniel Bowditch
|
Historical Sketch Nathaniel Bowditch (1773 - 1838) was the first American to
receive international recognition as a mathematician.
Moreover, he was the first to investigate a family of curves now
usually named for the French physicist, Jules-Antoine Lissajous.
Lissajous independently published his work much later in 1857.
|
|
|
|||
| http://www-history.mcs.st-and.ac.uk/history/Curves/Lissajous.html | |||
| http://mathworld.wolfram.com/LissajousCurve.html | |||
| Boyer, Carl B.,
revised by U. C. Merzbach, A History of Mathematics,
2nd ed., John Wiley and Sons, 1991. |
|||
| Eves, Howard,
An Introduction to the History of Mathematics,
6th ed,. The Saunders College Publishing, 1990. |
|||
| Gray, Alfred, Modern Differential Geometry of Curves and Surfaces with MATHEMATICA®, 2nd ed., CRC Press, 1998. | |||
| Sobel, Dava, Longitude:
The True Story of a Lone Genius Who Solved the Greatest Scientific
Problem of His Time, Walker and Co., 1998. |
|||
| Yates, Robert,
CURVES AND THEIR PROPERTIES, The National
Council of Teachers of Mathematics, 1952. |
|||
|