Back to ...

Curve Bank Home
Classics Index Page

NCB logo
 Deposit # 86
Algebraic Curves, MATHEMATICA® Animations

"Singular Points" or "Singularities" occur in mathematics when a curve intersects itself or creates a cusp at the particular point. It is said that the curve at this point is in some sense not "well-behaved."  In the following curves the misbehavior consists of partial derivatives of x and y equaling zero.


THE NODE

Node animation
Node
The node is located at the origin of the curve. It is characterized by the equation x3-x2+y2=0.
This node is an ordinary double point.
It has distinct tangents: x+y=0 and x-y=0.




ISOLATED

Isolate node
Singularity
The origin above is an "isolated" point of the curve. It is obtained from the equation x3+x2+y2=0.
The tangets of the curve are : x+iy=0 and x-iy=0.




CUSP


Cusp


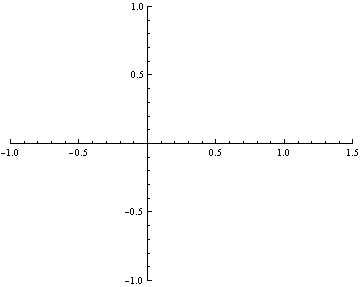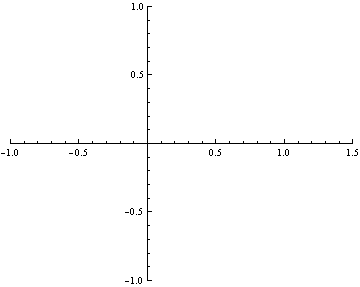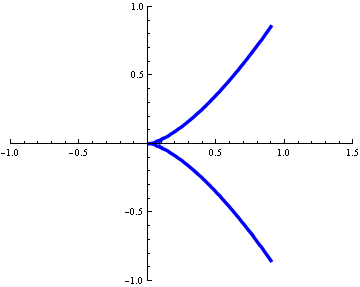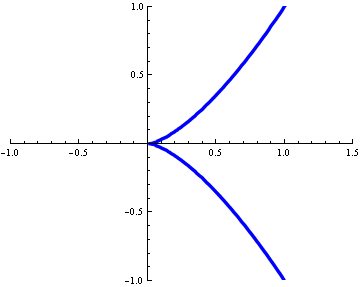
The cusp or spinnode is another type of singularity which is, too, a double point. It is characterized by two branches of a curve meeting where the tangents are equal to one another. This cusp has the equation x 3-y 2=0.




TACNODE


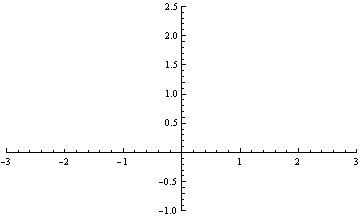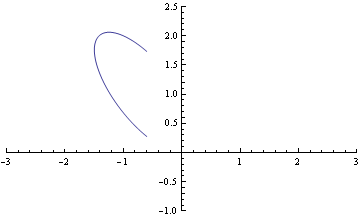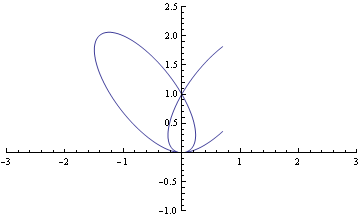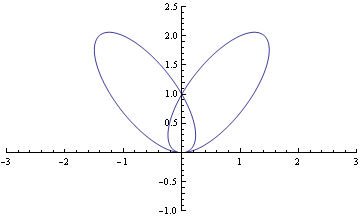
Tacnode


The curve is called a tacnode, it is also a double point like the cusp. The tacnode is a point on a graph where the two, or possibly more, osculating circles meet at a tangent. The tacnode below is at the origin. The osculating part of the graph comes from the latin circulum osculans, which means " kissing circles ".
It's equation is 2x 4-3x 2y+y 2-2y 3+y 4=0.




RAMPHOID


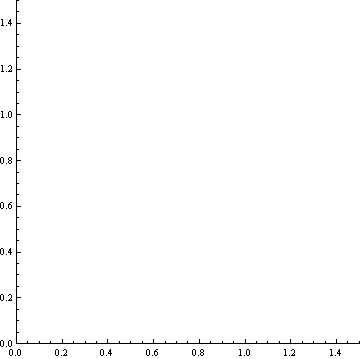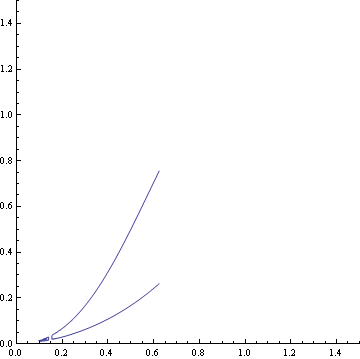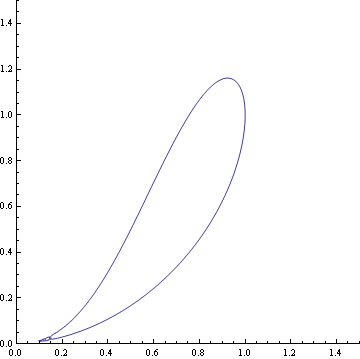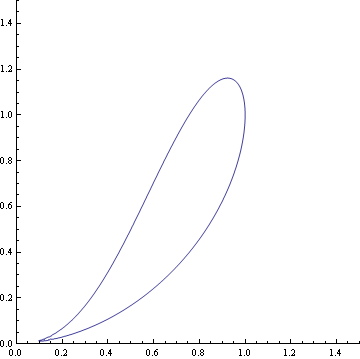
Ramphoid


A ramphoid is also a type of cusp. It comes from the greek "ramphos" which means "the crooked beak of birds, especially birds of prey, " and that is what the curve looks like. Also ramphoids are generally curves that have both branches one one side of the tangent. The equation is x 4 +x 2 y 2 -2x 2 y-xy 2 +y 2 =0.




TRIPLE


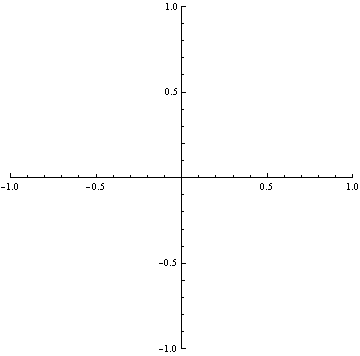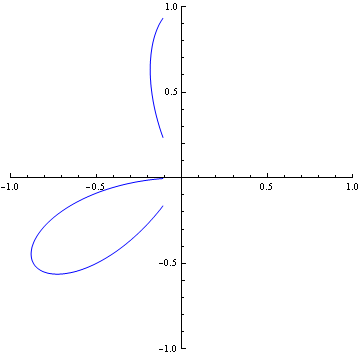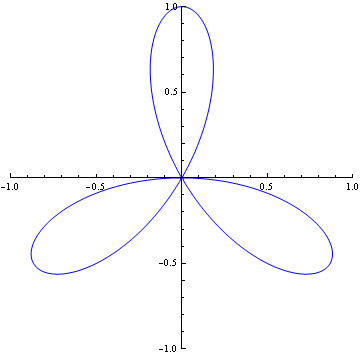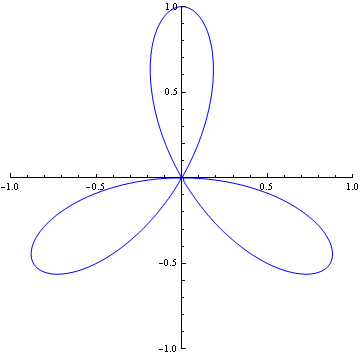
Triple point


The origin above is is an ordinary triple point it is represented by (x 2+y 2) 2+3x 2y-y 3=0





CLOVER


Clover


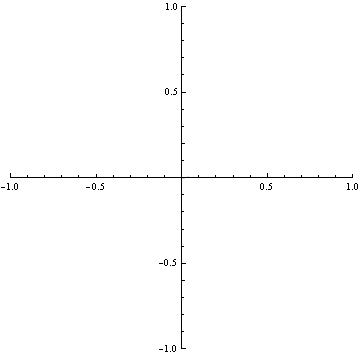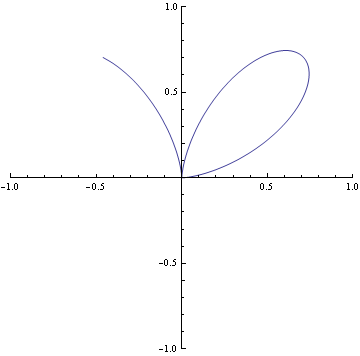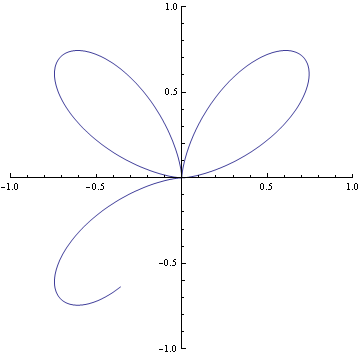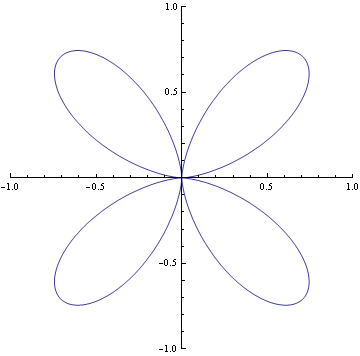
The origin above is is an ordinary quadruple point and it has multiplticty four. It's tangents coincide in pairs. And it is represented by (x 2+y 2) 3-4x 2y 2=0.




FINAL


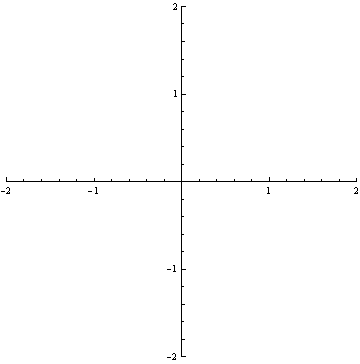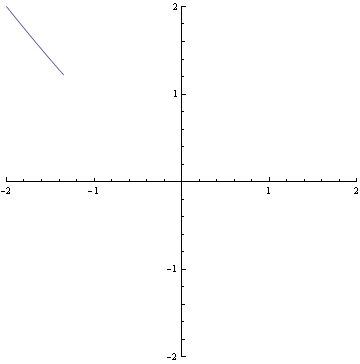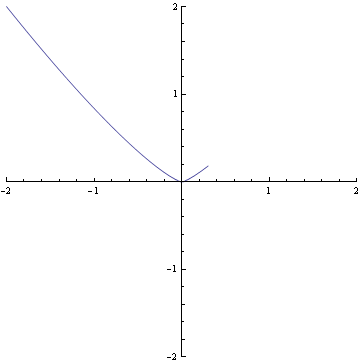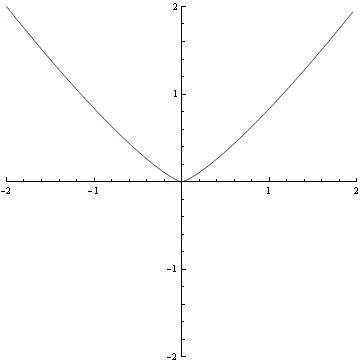
High multiplicity point


Here is another singular point with higher multiplicity. It is represented by x 6=x 2y 3-y 5=0. and the origin has one triple tangent and two simple tangents.


Reference
Robert John Walker, "Singular Points" in Algebraic Curves, Princeton University Press, 1950, pp. 56-58.


DOWNLOAD


All the animations and images above were created in MATHEMATICA v6.0®
To view the notebook with all of the animations and source code click here
Notebook and source code
If you do not have MATHEMATICA® you can download the Notebook viewer.
MATHEMATICA® READER

Index button
 NB Home button This page was contributed by

Oksana Maeva 2008.
Signature