|
|
|
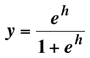
This is an
example of logistic regression,
a continuous function. However, note
that a rectangle could be drawn under
any
one of the jumps in the curve.
When the pixels are smoothed
to
represent continuous data,
the graph is named an ogive curve.
When the second derivative is zero, the
slope is zero, and we have a "point of inflection."
Segment at the point of
inflection.
Note:
Study the graphing calculator image. Notice the graph
is not smooth and continuous. It is
conventional to define the cumulative frequency for all values of x up
to and including the given right end-point value. Thus, an
ordinate represents the sum
of all frequencies up to and including a corresponding frequency
in a frequency distribution. Your calculator
or software will
calculate a value of y
to be mapped with the corresponding value of x but must "jump" to represent a
continuous
function.
|
|
|
|
In
mathematics, the name ogive is
applied to any continuous cumulative frequency polygon and is
derived from its resemblance to the shape of architectural molding
known
as the ogee pattern.
Another way to
express this is to say an ogive curve has the shape of an
elongated S.
Also, it is sometimes called a "double curve"
with one portion being concave and the other being convex.
|
Be
careful in drawing a distinction between ogive and ogee, especially when
applied to
architecture. Conflict abounds in the literature and common usage.
For example, a 1954 edition of the Funk and Wagnalls dictionary
uses the term ogive
to describe the arch over doorways and windows as
illustrated by the north entrance to Westminster Cathedral,
London. "This sense is wholly arbitrary and is unknown before
1830, when it appears to have been adopted through a misunderstanding,
but it is of frequent occurrence since that date."
A mathematician viewing the ogive
pattern as seen in the window notes a cusp at the apex. The slope
is undefined at the point of a cusp.
The same dictionary defines ogee
as a "cyma reverse molding" and having a "section in reverse" or as a
"long S
curve" and continues by
using the examples of "ogee doorway" and "ogee window."
|

|
|
Proud
owners of
early
American mantle clocks use the term ogee to describe a weight-driven
pendulum mechanism in a rectangular case. The owners know the
internal weight on the
left must be wound in a clockwise direction while the weight on the
right is hoisted using a counterclockwise direction, thereby aping the
pattern of arches in cathedrals.
(The Smithsonian
Institution is on the middle panel.)
|

|
|
Other Examples
|
The Instituto Veneto di Scienze, Lettere ed
Arti in Venice.

The ogive curve is sometimes
called the "Venetian Arch."
|
Another early
American clock
with an "ogee" mechanism and an "ogive" case.

|
|
|
|
Classic
Birthday Problem ~ An Ogive Curve
What is
the probability that at least two people in a given group will
have the same birthday? For this problem we
ignore leap years and assume that a person's birthday can fall on any
day with the same probability.
Numerator:
If the n persons
are to have different birthdays, the the first person can be born on
any of the 365 days, but the second person can only be born on one of
the remaining 364, the third person on the remaining 363 days, etc.
Denominator: As there are n
people and 365 different days, there are 365 n possible ways in which the
people
might have their birthdays.
For a group as small as 23 people, the probability becomes less than
one-half, or less than "50-50" that two people will not have the same
birthday. In other words, it is more likely to find that two
people will
have the same birthday.
|
|
References
| For
those who have MATHEMATICA®, . . .Alfred Gray, Modern Differential Geometry, 2nd
ed., CRC Press, 1998, p. 909 has logistic code. |
 |
|
J. F.
Kenney and E. S. Keeping, Mathematics
of Statistics: Part One,
D. Van Nostrand Co., 1954, pp. 29-31.
|
| Eric W.
Weisstein, CRC Concise Encyclopedia
of Mathematics, CRC Press, 1999, p. 1267. |
|
|
|