| Back to . . . Deposit #54 |
 Osculating Circles for Curves in a Plane |
 |
|
The word
"osculate" means "to kiss." A succession of circles that converge
to snuggly "kiss" a curve are said to be osculating circles. They
are also known as the Circle of
Curvature.
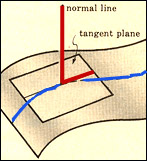
 The
tangent to a point on a curve was applied by the earliest
investigators to study the derivative and thus Calculus. Just as
the tangent line
approximates a curve at a point, the osculating circle is an even
better approximation by capturing the curvature. The
tangent to a point on a curve was applied by the earliest
investigators to study the derivative and thus Calculus. Just as
the tangent line
approximates a curve at a point, the osculating circle is an even
better approximation by capturing the curvature. |
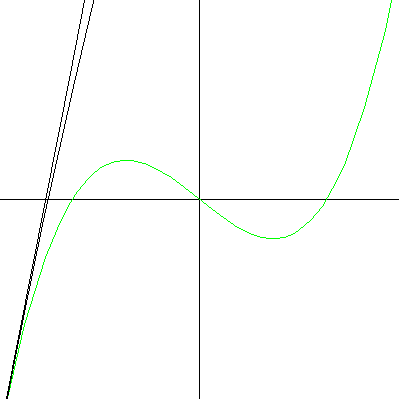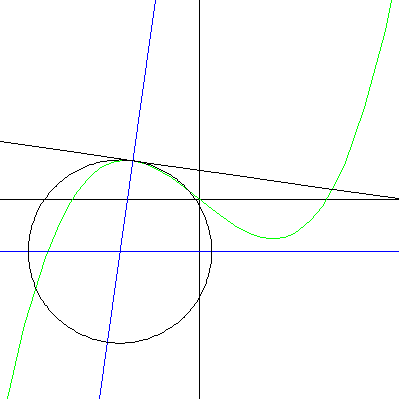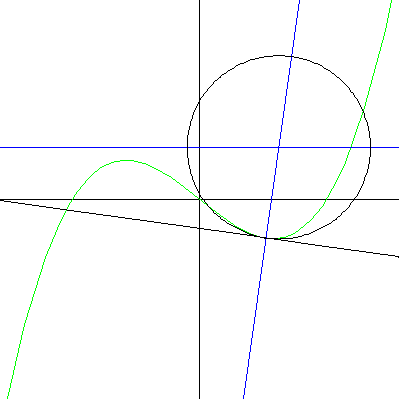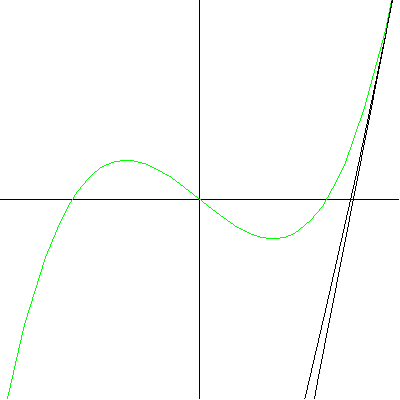 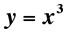 Note that at the point of inflection (second derivative), the tangent must jump across the curve; thus, the circle also jumps across this curve. Replay the animation to watch the jump at (0,0). In our MATHEMATICA® animations, both the tangent and normal lines are drawn at the point of contact of the curve and the circle. |
Our
animations feature several
Classic
Curves We ask you to
recall the construction for circumscribing a circle about a triangle. 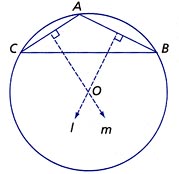
A minimum of
three points on the curve are
needed to determine, first the perpendicular bisectors, and then the
center and radius of the osculating circle. As the three
points on a given curve move closer together - converge to a single
point - the radius of the circle becomes the normal to the tangent at
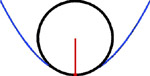
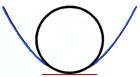
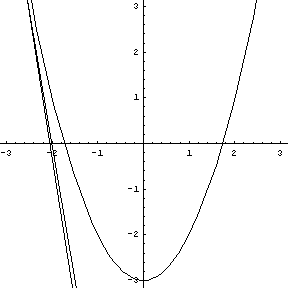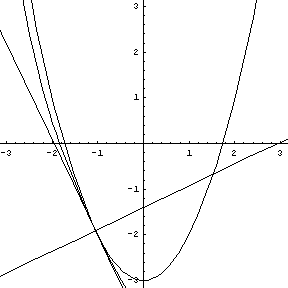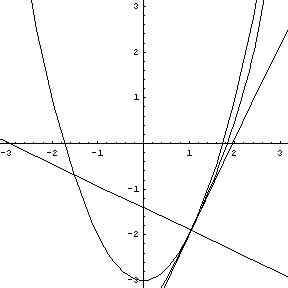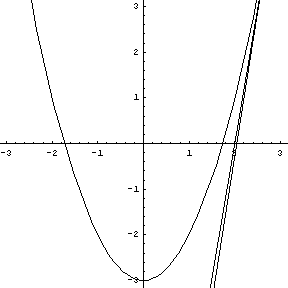
the point.  Play this animation. As the three
points on the parabola converge to the vertex, the circle of curvature
takes on a radius and center containing the normal to the point of
tangency.
|
 |
 y = sin (x), a tangent, normal, and osculating circle. |
In our MATHEMATICA® animations, both
the tangent and normal lines are drawn at the point of contact of
the curve and the circle.
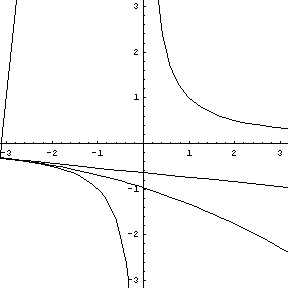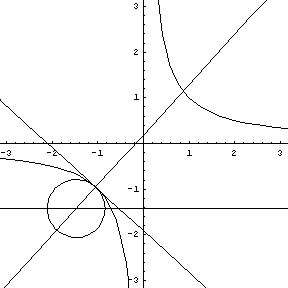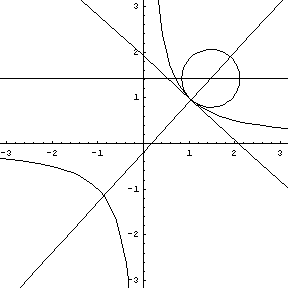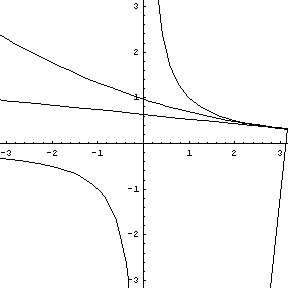 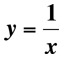 Replay this animation. |
 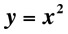 Replay this animation. |
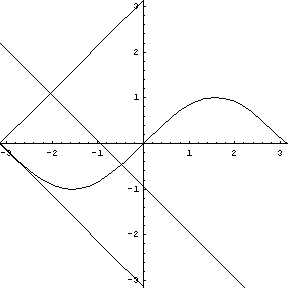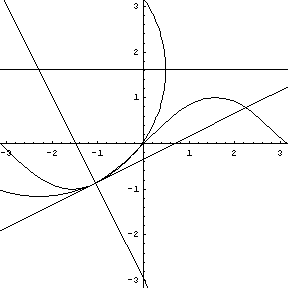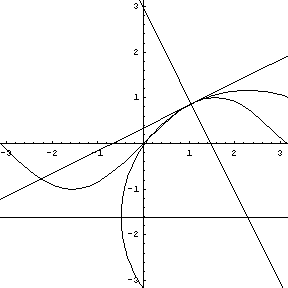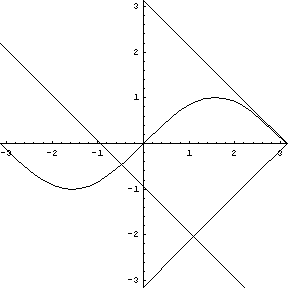 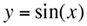 Replay this animation. |
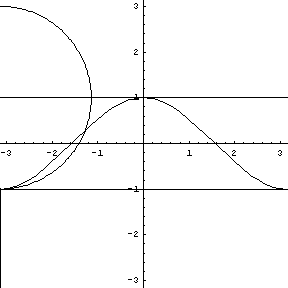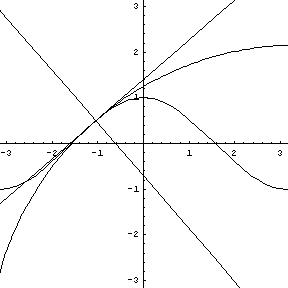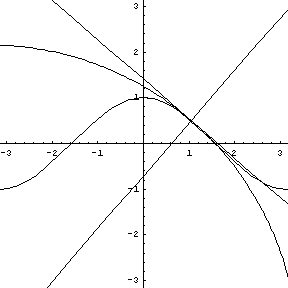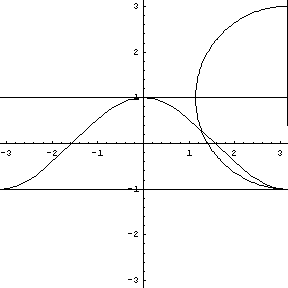  Replay this animation. |
 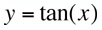 |
|
|
Suggestions
for the MATHEMATICA® code are on this link. |
|

 .
.
