| Back to . . . |  The Parabola of Fermat: A Member of the Spiral Family of Plane Curves. . . . |
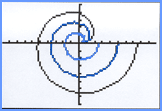 The Parabola of Fermat with a = 1, 2, or 3. |
 Replay the animation |
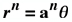 For n = 2, 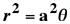 The Spiral Family of Curves is analogous to the Cartesian 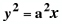 This parabolic curve was investigated by Fermat as early as
1636. There are plus and minus values of r for any positive
angle. Thus the equation for the single spiral may have the form
. . .
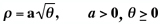 . . |
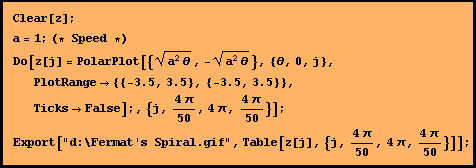 The spiral curves are easily entered and modified on a graphing calculator. |
 Eadem mutata resurgo. I shall arise the same though changed. |
Other Animations with MATHEMATICA®Code
Historical Sketch on Spirals
The name spiral, where a curve winds outward
from a fixed point, has been extended to curves where the tracing
point moves alternately toward and away from the pole, the so-called sinusoidal
type. We find Cayley's Sextic, Tschirnhausen's Cubic, and
Lituus' shepherd's (or a bishop's) crook. Maclaurin, best known
for his
work on series, discusses parabolic spirals in Harmonia Mensurarum (1722).
In architecture there is the
Ionic capital on a column. In nature, the spiraled chambered
nautilus is associated with the Golden Ratio, which again is associated
with the Fibonacci Sequence. |
|
|
|||
| http://www-history.mcs.st-and.ac.uk/history/Curves/Fermats.html | |||
| Boyer, Carl B., revised by U. C. Merzbach, A History of Mathematics, 2nd ed., John Wiley and Sons, 1991. | |||
| Eves, Howard, An Introduction to the History of Mathematics, 6th ed,. The Saunders College Publishing, 1990. | |||
| FERMAT'S THEOREM, math HORIZONS, MAA, Winter, 1993,
p. 11. |
|||
| Gray, Alfred, Modern Differential Geometry of Curves and Surfaces with MATHEMATICA®, 2nd ed., CRC Press, 1998. | |||
| Katz, Victor J., A History of
Mathematics, PEARSON
- Addison Wesley, 2004. |
|||
| Lockwood, E. H., A Book of Curves, Cambridge University Press, 1961. | |||
| McQuarrie, Donald A., Mathematical
Methods for Scientists and Engineers, University Science Books,
2003. |
|||
| Shikin, Eugene V., Handbook and Atlas of Curves, CRC Press, 1995. | |||
| Yates, Robert, CURVES AND THEIR PROPERTIES, The National Council of Teachers of Mathematics, 1952. | |||
|


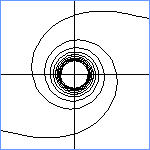
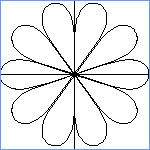
 From the
legendary Delian problem in antiquity to modern
freeway construction, spirals have attracted great mathematical talent.
Among the more famous are
From the
legendary Delian problem in antiquity to modern
freeway construction, spirals have attracted great mathematical talent.
Among the more famous are