| Back to . . . .
 Curve Bank Home Curve Bank Home
Dr. Paul Chabot
Department of Mathematics
California State Univ.,
Los Angeles
|

Polar Graphs
Create Your Own Polar
Animations Using Maple!
|
| The graphics in this deposit were
created using Maple software

|
NCB Deposit # 29
|
A
Sampler
for the Student. To view a larger
continuous
animation, click on the image in each cell.
Please be patient!
This is a large file with many
graphics that
may require several seconds to load.

|
The above animations are the
polar graphs of . . .
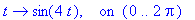
The middle image takes the
equation from polar form to rectangular coordinates.
Dr. Chabot's Maple Work Sheets
can be easily altered to graph any polar function on any
domain. [Only one line of code for each change.] The
instructions are in the Work Sheets linked on the left. The
provision is that you must own a copy of Maple.
|
These polar
graphs have
the shape of a petalled flower. They were named Rhondonea
in the 18th century by the Italian mathematician Guido Grandi.
Today
we call this a Rose polar graph.
In our equation, n
= 4,
an even number. If n is even, the Rose will
have
2n petals. If n is odd, the rose will have the odd number
of n-petals.
|
| Shikin, Eugene V., Handbook
and Atlas of Curves, CRC Press, 1995, pp. 304-306.
Yates, R. C., Curves
and their Properties, NCTM, 1952. Also in A Handbook on
Curves and their Properties, various publishers including the NCTM.
Weisstein, Eric. W., CRC
Concise Encyclopedia of MATHEMATICS, Chapman & Hall/ CRC, 2nd
ed., 2003.
|
For Mathematica® code that
will create polar graphs:
Gray,
A., MODERN DIFFERENTIAL GEOMETRYof Curves and Surfaces with
Mathematica®, 2nd. ed., CRC Press, 1998.
< http://mathworld.wolfram.com/Rose.html
>
|
|