|
Math in the news: Are there an infinite
number of
pairs of "twin primes?"
For the student . . . .
 |
 |
Background . . . .
Twin
primes are
pairs of prime numbers that only differ by two.
| Examples: |
3
and 5 |
| |
5
and 7 |
| |
11
and 13 |
| |
17
and 19 |
| |
29
and 31 |
| |
41
and 43 |
| |
59
and 61 |
Until
recently, it had been conjectured that there are infinitely many twin
primes. If the probability of a random integer n and the
integer n+2 being prime were statistically independent
events, then it would follow from the prime number theorem that there
are about n/(log n)2 twin
primes less than or equal to n. These probabilities are not independent.
A famous
team of British mathematicians - hmm, another pair so to speak, Hardy
and Littlewood, conjectured that the correct estimate should be the
following:
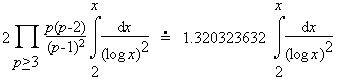
But
conjecture is not a proof. Recently, in March
2003, a new team of mathematicians - Dan Goldston of San
Jose State University in California and Cem Yalcin Yildirim of Bogazici
University in Istanbul, Turkey - announced they had at least made
progress in proving the suspicion that pairs of primes keep going off
to infinity.
Goldston
attacked the proof in a novel manner. In a sense, he avoided the
question by working on a more manageable piece of the problem:
Taking into account the fact that the
larger numbers become, the sparser the occurrence of primes, is
it possible to always find prime numbers that may not be twins, but
that are much closer together than average?
Goldston
and Yildrim believe they can prove the answer is an emphatic "Yes!"
|

|
|
Significance
The Prime Number theorem is seemingly about as intertwined
with the Zeta function as anything can be.
Thus, the distribution of primes is closely related to one
of the
most renowned unsolved questions in mathematics, the Riemann
hypothesis, which
concerns an infinite sum of numbers called the Zeta function.
Hilbert listed the Riemann hypothesis as the eighth problem
in his famous address before the Paris Congress in 1900. Smale
listed it
first in his selection of unsolved problems in 2000.
Currently, the Clay Mathematics Institute is offering $1
million to anyone who can prove the Riemann hypothesis.

Experts believe that the new result may pave the way for a
proof of the Zeta function and thus, the Riemann hypothesis.
|
For several years Chris K. Caldwell of the University
of
Tennessee, Martin, has created and maintained an indispensable web site
on
prime number theory. The NCB was lucky to have had his timely
Deposit
# 19 a few weeks before the announcement of Goldston and Yildrim's
new work.
Unfortunately, Goldston and Yildrim had to withdraw their
findings. But the search for primes continues to fascinate
researchers.
The “largest” known prime on May, 2004 was also the forty-first known
Mersenne prime. This prime was found by Josh Findley of the
National Oceanic and Atmospheric Administration. The number can
be expressed as
and when written
out, is made up of 7,235,733 according to the Great Internet Mersenne
Prime Search, or GIMPS.
On February 26, 2005
a still larger prime was announced by GIMPS organizer George Woltman.
He reported the forty-second Mersenne prime with the work being
verified by Tony Reix. This prime has 7,816,230 digits, the
largest of any type, and may be expressed as
The NCB recommends the following sources:
|
| How Many Primes Are There? See < http://www.utm.edu/research/primes/howmany.shtml
> |
| Frequently Asked Questions about Prime Numbers.
See < http://www.utm.edu/research/primes/notes/faq/
> |
| What are the ten largest known "twin
primes?" See < http://www.utm.edu/research/primes/largest.html#twin
> |
"Great Internet Mersenne Prime Search" See <
http://www.mersenne.org
> and Focus, The
Newsletter of the Mathematical Association of America, vol. 24,
February, 2004, p. 4.
|
Jeffrey J.
Wanko, "The Legacy of Marin Mersenne," Mathematics Teacher, vol. 98, No.
8, April, 2005, pp. 525-529.
|
| and from the BBC News on April 4, 2003,
see < http://news.bbc.co.uk/2/hi/science/nature/2911945.stm
> |
  |
|