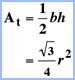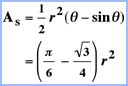| Back to . . .
Deposit #53 |
 Curves of Constant Width and Reuleaux Polygons |
 |
| Observe the path
of the triangle as
it rotates. First, the path of the boundary is not a square at
the four corners. But because the triangle rotates within a
square, it is the basis for a square
drill bit. The behavior of the center is also fascinating. The center does not remain fixed and thus traces a path composed of four arcs of an ellipse. |
 |
This section
features the
Constant Width Curves They
are also known as Reuleaux Polygons,
most often the triangle, or "Rollers."
Their well-known application is found in the Wankel Engine
|
|
|
 |
 |
Historical Sketch:
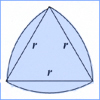
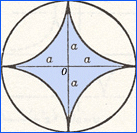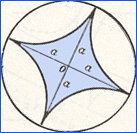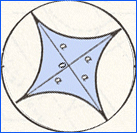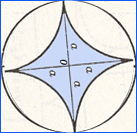A constant width curve is a planar convex oval with the
property that
the distance between two parallel tangents to the curve is
constant. Visualize a
circle inscribed in square with the circle rolling, or rotating in the
square. The diameter of the circle is the same as the width of
the square. The width of a closed convex curve is defined to be
the distance between the parallel lines bounding it. The parallel
lines of the square are sometimes called "supporting lines."
Please note, the inscribed asteroid does not fit the definition.Some background is helpful. Unlike many plane curves, the constant width and Reuleaux polygon investigations are rooted in machine design and engineering. Moreover, compared to the history of most plane curves, this work is relatively young.
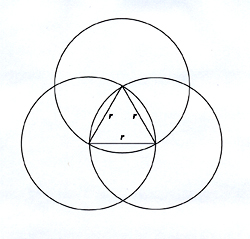
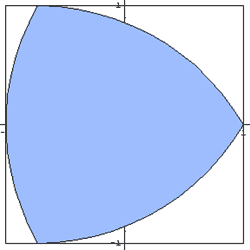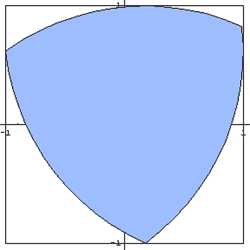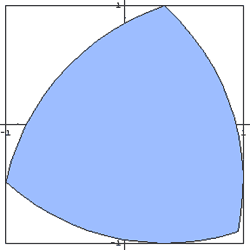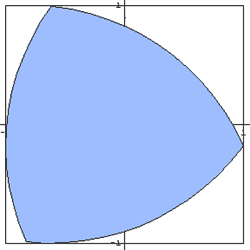
Franz Reuleaux (1829 - 1905) recognized that simple plane
curves of constant width might be constructed from regular polygons
with an odd number of sides. Thus, triangles and pentagons are
frequently constructed using a corresponding number of intersecting
arcs.
In engineering, Felix Heinrch Wankel (1902-1988) designed a
rotor engine which has the shape of a Reuleaux triangle inscribed in a
chamber, rather than the usual piston, cylinder, and mechanical
valves. The rotor engine, now found in Mazda automobiles has 40%
fewer parts and thus far less weight. Within the Wankel rotor,
three chambers are formed by the sides of the rotor and the wall of the
housing. The shape, size, and position of the chambers are constantly
altered by the rotation of the rotor, i.e., the Reuleaux triangle or
deltoid. _
 |
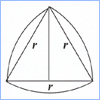
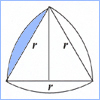
Areas
Total Area of a Reuleaux Triangle  |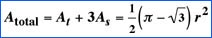
| Additional
MATHEMATICA® CODE |
|||
|
|
|||
|
For information on the Wankel engine: < http://en.wikipedia.org/wiki/Wankel_engine > |
|||
| http://mathworld.wolfram.com/ReuleauxTriangle.html | |||
| Eves, Howard, AN INTRODUCTION TO THE HISTORY OF MATHEMATICS, 6th ed., Saunders College Publishing, 1992. | |||
| Gray, Alfred, Modern Differential Geometry of Curves and Surfaces with MATHEMATICA®, 2nd ed., CRC Press, 1998. | |||
| Reuleaux, Franz, The Kinematics of Machinery, trans.
A. Kennedy, Dover, 1963 (reprint of 1876 translation of 1875
German original). |
|||
| Wagon, Stan, MATHEMATICA®IN ACTION, W. H. Freeman and Co. ISBN 0-7167-2229-1 or ISBN 0-7167-2202-X (pbk.) | |||
| Wagon, Stan, MATHEMATICA®
IN ACTION, 2nd ed., Springer-Verlag, 2000. ISBN
0-387-98684-7 |
|||
|
