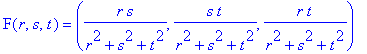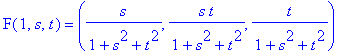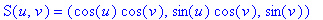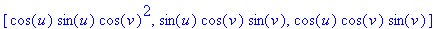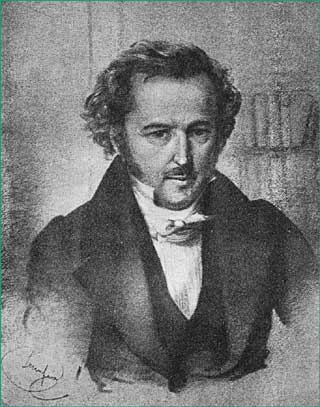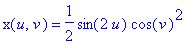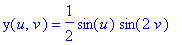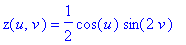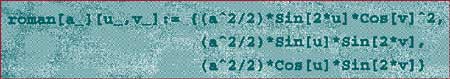| Back
to . . .
|

Dr. Adam Coffman Department of Mathematical SciencesIndiana University - Purdue University Fort Wayne http://www.ipfw.edu/departments/coas/depts/math/coffman/steinersurface.html |

Surfaces and Computer Graphics |
Steiner Roman Surfaces
| Jakob Steiner (1796 - 1863 ) was a Swiss mathematician who became a professor at the University of Berlin. He visited Rome in 1844 where he developed the concept of a surface that we now call Steiner's Roman Surface. Its special properties are as follows: |
| 1. The real projective plane can
be constructed
as a topological surface, by attaching a Mobius strip along its
circular
edge to the circular edge of a disk. Another construction of the
real
projective plane is to identify antipodal (diametrically opposite)
points
on a sphere. There is no way to represent this surface in three
dimensions
without the surface intersecting itself. 2. Steiner's Roman surface is one
representation of the real projective plane, and it intersects itself
along three line
segments. 3. These three line segments meet
each other at a triple point, and their six endpoints are called pinch
points. 4. Another interesting property of
Steiner's Roman surface is that at each of its points, there are
infinitely many conic section curves which go through that point and
lie on the surface. 5. The Roman surface can be defined by parametric functions which are quotients of quadratic polynomials in three variables:
Notice that the equations are "homogeneous," which means that for any non-zero constant c,F(r,s,t)=F(cr,cs,ct). Any surface defined by homogeneous quadratic rational
functions like this is called a "Steiner surface," and the Roman
surface is one of 10
types, as classified by Coffman, Schwartz, and Stanton. 6. The homogeneous property of the parametric equations means that we don't have to use all three domain variables (r,s,t), but can use just two parameters to describe the surface. One two-parameter equation for the Roman surface is:
7. Another two-parameter equation for the Roman surface is to use points (r,s,t) on the unit sphere, which itself has parametric equations
Since r^2+s^2+t^2=1, the composition of the Roman map F and the Sphere map S, or F(S(u,v)), is
Since F(r,s,t)=F(-r,-s,-t), the antipodal points on the sphere have the same image. |
 Steiner's first major publication ( Systematische Entwicklung der Abhängigkeit geometrischer Gestalten von einander . . ., part 1, Berlin 322pp., 1832) laid the foundation for modern synthetic geometry. Very soon after this volume appeared numerous honors were bestowed on him. They included an honorary degree from the University of Königsberg (1833) and a new chair of geometry at the University of Berlin. His Roman Surface papers appeared near the peak of an outstanding career.
|
The implicit equation:
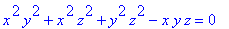 The composition simplifies to
|

The code is as follows:
|
|
|
| For an Index of Steiner Surface images, see < http://www.ipfw.edu/departments/coas/depts/math/coffman/steinersurface.html > For Roman Surfaces from the University of Minnesota Geometry Center, see < http://www.geom.umn.edu/zoo/toptype/pplane/roman/ >. For an array of surfaces, see
the Tore Nordstrand Gallery from Norway <
http://www.uib.no/People/nfytn/mathgal.htm
>. Coffman, A., Schwartz, A., and Stanton, C. "The Algebra and Geometry of Steiner and Other Quadratically Parametrizable Surfaces." Computer Aided Geometric Design, 13, 257 -286, 1996. Gray, A., MODERN DIFFERENTIAL GEOMETRY of Curves and Surfaces with MATHEMATICA®, 2nd. ed., CRC Press, 1998. See p.332 and p.963. Shikin, Eugene V., Handbook and Atlas of Curves, CRC Press, 1995. Steiner's papers were
collected, edited
by another famous mathematician, Karl Weierstrass, and published by the
Prussian
Academy of Sciences. |