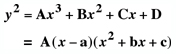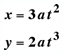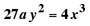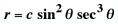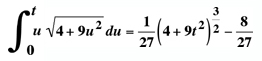|
|
Interesting Facts . . . .
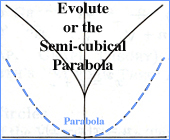
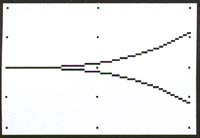
The Semi-cubical Parabola is
probably the first curve in our NCB collection whose history is more
fascinating than its mathematics. William Neile (1637-1670)
discovered and rectified - measured - its arc length. His
far more famous professor, John Wallis (1616-1703), published Neile's
method in De Cycloide (1659).
Wallis was a charter member of the Royal Society of London that he had
helped to organize. With a Cambridge education followed by his
appointment as Savilian Professor of Geometry at Oxford, Wallis was a
natural leader in the mathematics community. In 1655 he published
two major papers, one in analytic geometry and the other in infinite
analysis. Most agree these were the two most important research
areas of their generation. When his student, Neile, managed to
not only discover a new curve but measure its arc length, Wallis
published the results giving Neile full credit. Neile was only
22. In 1663, Neile was elected a Fellow of the Royal Society, and
thus became both one of its earliest and youngest members.
Later, on the continent, both Leibniz and Huygens investigated the
problem of finding a curve down which a particle might descent, under
the force of gravity, by falling equal vertical lengths in equal time
intervals with an initial velocity different from zero. In 1673
Huygens' greatest publication, Horologium
oscillatorim, presented, among other things, his findings on
evolutes and involutes show the
evolute of a parabola is a semi-cubical parabola. The evolute of
a curve is the locus of its centers of curvature.
Broad
observations are important. This was the milieu - the
mathematical firmament - from which emerged modern physics and
calculus. If this reads like your early physics and calculus
education, that is exactly what was in the wake. To quote E. T.
Bell,
"It was inevitable after the work of
Cavalieri, Fermat, Wallis, Barrow, and others that the calculus should
presently get itself organized as an autonomous discipline. Like
a crystal being dropped into a saturated solution at the critical
instant, Newton solidified the suspended ideas of his time, and the
calculus took definite shape."
E. T. Bell, Men of Mathematics
|
Unfortunately, Neile died in 1670 without
knowing that Huygens had bestowed a significant finding upon his
work. He was only 32.
Students at Oxford University are very loyal to their college.
Neile had been at Wadham, the same college as our contemporary today,
Sir Roger Penrose.
|
Equations for the Semi-cubical Parabola - General
Equations
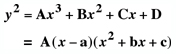
have fanciful names resembling botanical terms
depending on the relative values of the constant terms A, B, C,
and D.
For the parametric
equations
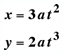
the corresponding Cartesian equation is
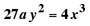
and a polar equation is
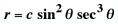
|
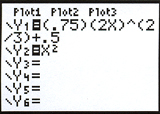
This particular
family of curves is easily entered on a graphing calculator. May
we remind you that to graph in the function mode of
y1 =
, you must enter separate formulas for the upper and lower
portions of the curve. In addition to needing an algebraic
expression for a function, one must also take a square root with two
options ( + ).
Both must be considered.
|
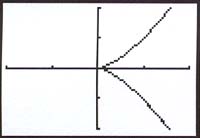
Cartesian
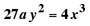
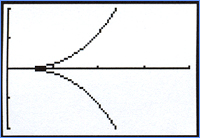
In this equation
the x-axis is a line
of symmetry, but for a good view of the cusp at (0,0), we suggest
you turn off the axes on your graphing calculator.
|
Polar
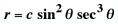
Parametric
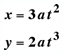
|
Arc
Length
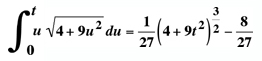
While calculating the arc length for a semi-cubical parabola gave Neile
lasting recognition in the history of mathematics, we no longer use his
method to compute. We apply the techniques of modern calculus
which, of course, he could not have known.
Also
please note, others had in fact calculated lengths for transcendental
(cycloid or logarithmetic spiral) type curves.
See [Gray, pp. 21-22 and Lockwood, p. 11
for a longer discussion.]
|
|
|
Useful Links and Books
|

John Wallis, F.R.S.
(1616-1703)
 Christian Huygens
Christian Huygens
(1629-1695)
|
| http://www-history.mcs.st-and.ac.uk/history/Curves/Neiles.html |
Bell, E. T., Men of Mathematics, Simon and
Schuster, 1937, p. 118.
|
| Boyer, Carl B., revised by U. C. Merzbach,
A History of Mathematics, 2nd ed., John Wiley and
Sons, 1991. |
| Eves, Howard, An Introduction to the
History of Mathematics, 6th ed,. The Saunders College Publishing,
1990. |
Gray, Alfred, Modern
Differential Geometry of Curves and Surfaces with MATHEMATICA®, 2nd ed., CRC Press, 1998,
pp. 21-22.
|
Katz, Victor J., A History of
Mathematics, PEARSON
- Addison Wesley, 2004.
|
| Lockwood, E. H., A Book of Curves,
Cambridge University Press, 1961. |
| Shikin, Eugene V., Handbook and Atlas
of Curves, CRC Press, 1995. |
| Yates, Robert, CURVES AND THEIR
PROPERTIES, The National Council of Teachers
of Mathematics, 1952 |
|
|