Back to . . .    Curve Bank Home  NCB Deposit  # 14 Steve Mathias steve@mathias.org

Sphericons . . . . . .a new solid shape. Two cones with a twist.

This section . . .

Begin with two cones. Slice the cross-section so as to produce a square.  Use the trig proportions for a 45o - 45o - 90o triangle where the diameter of the cone becomes the hypotenuse of a plane triangle. Rotate one of the sections. Reattach the two figures.

The sphericon is a double-cone, two identical cones joined base to base, but with a twist. It is easy to make. If you slice a double-cone along a plane that includes both vertices, you get a rhombic cross section, a parallelogram with four equal sides. If you use cones of just the right shape, you get a square cross section. Unlike all other rhombi, the square has an extra symmetry: rotate it through a right angle and it fits back into the same shape. So you can slice such a double-cone down the middle, rotate one of the halves through a right angle and glue the two pieces back together. This is the sphericon. Thanks to the twist, it is not a double-cone but a much more interesting beast.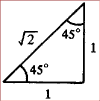 

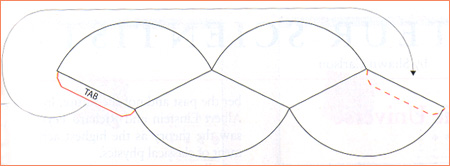
The sphericon can also be made from a single piece of thin card, cut to a shape made from four identical sectors of a circle joined together so that they face in alternate directions (see illustration). 

A very delightful property, or characteristic, of the sphericon is that it rolls! A cone placed on a flat surface rolls around in circles. A double-cone can roll in a clockwise circle or a counterclockwise one, but it rolls straight only if you rapidly bowl it or set it on rails. A sphericon performs a controlled wiggle, which on average is straight. First one conical sector is in contact with the flat surface, then the next. So as it moves forward it wiggles alternately to the left and right. It is especially interesting to start it at the top of a gradual slope and watch it wobble its way down. It has one continuous face, and one sphericon can roll around another ad infinitum. 

If two sphericons are placed next to each other, they can roll on each other's surfaces. Four sphericons arranged in a square block can all roll around one another simultaneously. And eight sphericons can fit on the surface of one sphericon so that any one of the outer solids can roll on the surface of the central one. 

One reason why the sphericon has such neat geometric properties is that its four "edges" - the lines where the component sectors meet - lie along four of the edges of a regular octahedron. The other four edges of the octahedron correspond to lines that bisect the vertex angles of the sectors. The octahedron, in turn, is closely related to the cube: if you put a dot in the middle of each face of a cube and join the dots by straight lines, you get an octahedron. And cubes, of course, stack in a regular manner to form a flat layer or fill three-dimensional space. 

Click here for an enlarged image suitable for printing a pattern. Steve Mathias has been experimenting with the shape and its variations.  He has made several sphericons, large and small, out of various materials.  He has used wire frames, and dipped them in bubble solution, with surprising and amazing results.  He has also made some that exhibit the characteristic wobbly roll, but are dramatically different in appearance. Recall the study of cones dates to Apollnius (262-190 BC) and other early Greeks.