Back to . . . 

Curve Bank Home

NCB Deposit # 51

Diana Venters
Elaine Krajenke Ellison

 dianaventers@aol.com
eellisonelaine@yahoo.com
 NCB logo

More Quilts:  A Sierpinski Curve
and other patterns . . . .

No Sewing Required
 		Sierpinski quilt
<>
Sampler Quilt

"Elaine Ellison and I have been making this series of mathematical quilts for almost 10 years.  Our interests in mathematical concepts for designs was a natural development from our interest in quilting which, by its nature is a pure application of geometry.  A century ago, quilters knew which shapes would tessellate.  Logarithmic spirals and fractal designs are the basis of early quilt patterns and before quilts, these designs were the inspiration for tile patterns. . . My interest in fractals began with my first sighting of Hilbert's curve."
Diana Venters, NCTM-San Diego, 1996 


From their Chapter on Linear Fractal Quilts
A Closer Look at One Quilt Pattern:  Sierpinski Curve

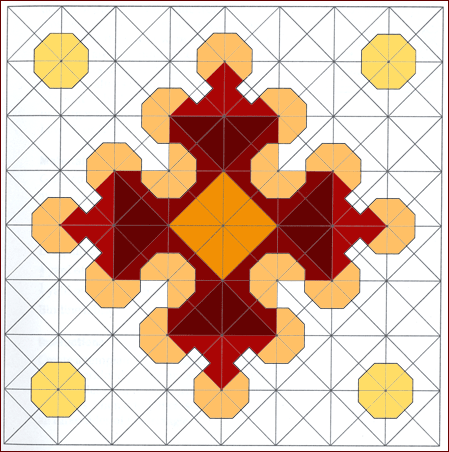
Unlike most well-known fractal curves, the sides of a Sierpinski curve are NOT formed upon the sides of a previous level; instead, its sides enclose a new shape at each level.  The first level is a square; the second level is an octagon.  The third level is a shape dominated by squares building upon alternating edges of the octagon.  The fourth level is dominated by octagons building upon the squares added in Level 3.  This alternating pattern of adding squares and octagons continues as higher levels are created.
Fractal levels
The following quilt created in Adobe Photoshop® is one possible illustration.  Venters and Ellison executed this pattern using calico fabrics in a dark/light color scheme.
Sample Sierpinski Quilt


Diana Venters and Elaine Ellison shared a passion for mathematics and a hobby of quilting.  Starting in the 1980s their interests merged into a collaboration that has produced almost 100 quilts, dozens of presentations at math conferences, and two books.  Convention goers will never forget their sessions.  See if you can identify the following classic patterns they have quilted:
1.   Golden spiral     
2.     Penrose tiling   
3.   Poincare circle      
4.     Escher tessellation    
5.   Spiral     
6.       Bashkara Proof of Pythagorean Theorem       


The images on this site are being used with permission of Key Curriculum Press, 1150 65th Street. Emeryville, CA 94608, 1-800-995-MATH,
          < http://www.keypress.com >.
For a collection based on a variety of famous mathematical patterns:
          Diana Venters and Elaine Krajenke Ellison, Mathematical Quilts, Key Curriculum Press, 1999.               ISBN 1-55953-317-X
For a collection of mostly fractal quilt patterns:
          Diana Venters and Elaine Krajenke Ellison, More Mathematical Quilts, Key Curriculum Press, 2003.     ISBN 1-55953-374-9
Home button

Pythagorean Tree
NCTM presentation
 Diana Venters
 and
Elaine Ellison