Click on the thumbnail
images below to see
experimental solar collectors
near Barstow, California
focus the sun's rays on a central
tower
where heat
is converted to electricity.



The famous Belvedere Apollo at the top
of this column is a Roman copy
of a much older Greek statue.
This marble is now in the
Pio Clementino Museum
at the Vatican (Rome, Italy).
The Burning Mirrows wall painting is from the Stanzino
delle Matematiche
in the Galleria degli Uffizi (Florence, Italy). Painted by Giulio
Parigi
(1571-1635) in the years 1599-1600.

|
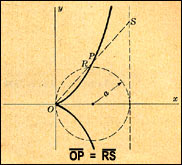
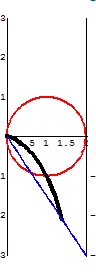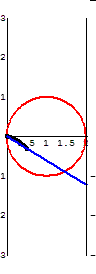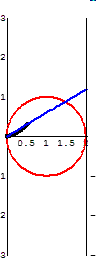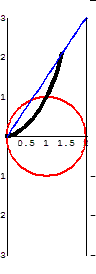
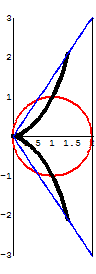
 The Cissoid of Diocles
The Cissoid of Diocles
Another attempt to solve one of the three famous construction problems from Antiquity.
Biographical Sketch
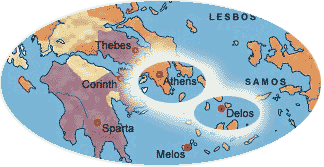
Diocles is one of many mathematicians who have attempted to construct a cube whose volume is exactly twice that of a given cube. This is often called the "Delian" problem or "duplication of the cube".
Legend:
A number of legends surround this construction challenge. The good citizens of Athens were being devastated by a plague. History records that in 430 BC they sought advice from the oracle at Delos on how to rid their community of this pestilence. The oracle replied that the altar of Apollo, which was in the form of a cube, should be doubled. Thoughtless builders merely doubled the edges of the cube. Unfortunately the volume of the altar increased by a factor of 8.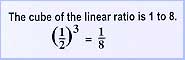 The oracle insisted the gods had been angered. As if to confirm this reprimand, the plague grew worse. Other delegations consulted Plato. When informed of the oracle's admonition, Plato told the citizens "the god has given this oracle, not because he wanted an altar of double the size, but because he wished in setting this task before them, to reproach the Greeks for their neglect of mathematics and their contempt of geometry." The oracle insisted the gods had been angered. As if to confirm this reprimand, the plague grew worse. Other delegations consulted Plato. When informed of the oracle's admonition, Plato told the citizens "the god has given this oracle, not because he wanted an altar of double the size, but because he wished in setting this task before them, to reproach the Greeks for their neglect of mathematics and their contempt of geometry."
The curve invented by Diocles in about 180 BC later appears in the works of Fermat, Roberval, Huygens, Wallis, Newton, and others. Problems on the cissoid's curvature, arc length, and areas bounded by its asymptote are found in modern calculus texts.
The cissoid also has much in common with the modern need to identify the focal point of a satellite "dish." The cissoid may be represented as the "Roulette for the Vertex of a Parabola", or the curve traced by a fixed point on a parabolic curve as that curve rolls without slipping along a second curve. Thus, if a fixed point on a parabola moves along a second parabola of similar dimensions, the vertex will become the cusp of a cissoid of Diocles. Moreover, if the cusp is taken as the inversion center, the cissoid inverts to a parabola.
 Diocles investigated the properties of the focal point of a parabola in On Burning Mirrors. There is a similar title in the works of Archimedes. The problem, then as now, is to find a mirror surface such that when it is placed facing the sun, heat is produced. Legend suggests Archimedes wanted to use parabolic mirrors reflecting the sun's rays to burn the sails of enemy ships. Diocles investigated the properties of the focal point of a parabola in On Burning Mirrors. There is a similar title in the works of Archimedes. The problem, then as now, is to find a mirror surface such that when it is placed facing the sun, heat is produced. Legend suggests Archimedes wanted to use parabolic mirrors reflecting the sun's rays to burn the sails of enemy ships.
Today, experimental solar collectors near Barstow, California, focus the sun's rays on a central water tower where heat is converted to electricity.
| A Brief Listing of references
that should
be in most university libraries.
Boyer, Carl B. A
History of Mathematics,
various editions and publishers.
Katz, Victor J. A
History of Mathematics,
2nd ed., Addison-Wesley, 1998.
Toomer, Gerald. Diocles
on Burning
Mirrors, Springer, 1976.
The History of Mathematics:
A Reader.
Edited by John Fauvel and Jeremy
Gray,
Macmillan and The Open University,
1987, pp.
181-182.
|

Plato
|
|







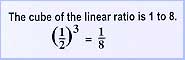 The oracle insisted the gods had been angered. As if to confirm this reprimand, the plague grew worse. Other delegations consulted Plato. When informed of the oracle's admonition, Plato told the citizens "the god has given this oracle, not because he wanted an altar of double the size, but because he wished in setting this task before them, to reproach the Greeks for their neglect of mathematics and their contempt of geometry."
The oracle insisted the gods had been angered. As if to confirm this reprimand, the plague grew worse. Other delegations consulted Plato. When informed of the oracle's admonition, Plato told the citizens "the god has given this oracle, not because he wanted an altar of double the size, but because he wished in setting this task before them, to reproach the Greeks for their neglect of mathematics and their contempt of geometry."  Diocles investigated the properties of the focal point of a parabola in On Burning Mirrors. There is a similar title in the works of Archimedes. The problem, then as now, is to find a mirror surface such that when it is placed facing the sun, heat is produced. Legend suggests Archimedes wanted to use parabolic mirrors reflecting the sun's rays to burn the sails of enemy ships.
Diocles investigated the properties of the focal point of a parabola in On Burning Mirrors. There is a similar title in the works of Archimedes. The problem, then as now, is to find a mirror surface such that when it is placed facing the sun, heat is produced. Legend suggests Archimedes wanted to use parabolic mirrors reflecting the sun's rays to burn the sails of enemy ships.