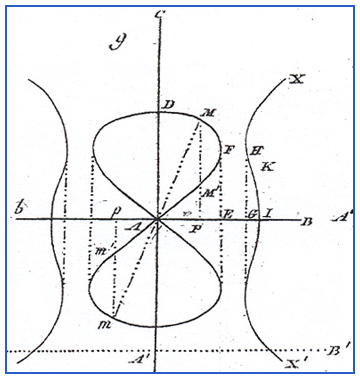
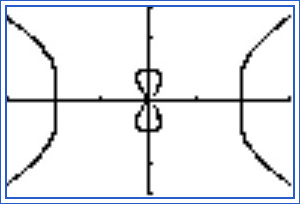
Anton, Howard and Rorres,
Chris, Elementary Linear
Algebra, Wiley, 2010, pp. 112-113.
|
Brown, B. H., La Courve du diable, The American Mathematical Monthly,
vol. 33 (5) May,1926, pp. 273-274.
|
Cramer, Gabriel, Introduction à l'analyse des lignes
courbes algébriques, Genève, Chez les
Frères
Cramer & Philibert, 1750.
|
Fladt, Kuno, Analytische Geometrie spezieller ebener
Kurven, Akademische Verlagsgesellschaft, 1962, p. 218.
Fladt uses "Die Teufelskcurve von Gabriel
Cramer." Teufelskcurve
may be translated as either the Devil's Curve or the Devil's hairpen.
|
Gray, Alfred, Modern Differential Geometry of Curves
and Surfaces with MATHEMATICA®, CRC Press, 1998, p. 92.
|
Lacroix, Silvestre
François, Traité du
calcul différentiel et du calcul intégral, vol.
1, Libraire pour les Mathématique, quaai des Augustins, 1797.
|
Koestler, Arthur, The SLEEPWALKERS, Arkana: Penguin
Books, 1989.
|
Rider, Paul R., The Devil's Curve and
Abelian Integrals, The American
Mathematical Monthly, vol. 34 (4) April, 1927, pp. 199-203.
|
| Stewart, James, Calculus: Early Transcendentals,
7th ed., Cengage: Brooks/Cole, 2012, p. 215. |
Venit, Stewart and Bishop,
Wayne, Elementary Linear Algebra,
4th ed., ITP Publishing Co., 1996, pp. 183-184. Proof: pp.
187-188.
ISBN: 053495190-2 |
Weisstein, Eric., Devil's Curve, < http://mathworld.wolfram.com/DevilsCurve.html
>.
Weisstein, Eric, CRC Concise
Encyclopedia of Mathematics, CRC Press, 1999, pp. 424 - 425.
|
Yates, Robert C., Curves and their Properties,
NCTM, 1974, p. 203. Yates writes, "This curve is found useful in
presenting the theory of Riemann surfaces and Abelian integrals."
Yates' reference to Brown's publication is invaluable.
|
|