

_______
The curve y = 1 / x in the
first quadrant
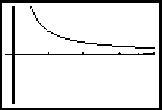
is rotated about the x-axis to generate a solid.
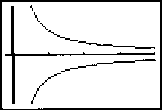
The y-axis is an asymptote and thus avoided by setting x>
1.

Torricelli's Trumpet or Gabriel's Horn
| Back to . . . | This section . . .
|

Biographical Sketch
Evangelista Torricelli ( 1608
- 1647
) was a student of Galileo. As a young man he studied in
Galileo's
home at Arcetri near Florence. Upon Galileo's death, Torricelli
succeeded
his teacher as mathematician and philosopher for their good friend and
patron, the Grand Duke of Tuscany.
Torricelli's own words fully describe his amazement at discovering an infinitely long solid with a surface that calculates to have an infinite area, but a finite volume. "It may seem incredible that although this solid has an infinite length, nevertheless none of the cylindrical surfaces we considered has an infinite length but all of them are finite." This "incredible" paradox prompted Torricelli to try several alternate proofs.
Torricelli was born a bit too
soon.
The study of infinitesimal was too new. Recall that Newton was
born
the year Galileo had died (1642) and Leibniz was yet four years
younger.
Unfortunately, Torricelli did not live to see the methods of calculus
fully
emerge to confirm his painstaking calculations largely based on his
friend
Cavalieri's "summation of plane slices" method.
|
 |




