| Back to . . .
 Curve
Bank Home
|
James
Clerk Maxwell ( 1831-1879 ) |
14 India Street
Edinburgh, Scotland
|
|
"One scientific
epoch ended and another began with James Clerk Maxwell."
"The special theory
of relativity owes its origins to Maxwell's
equations of the electromagnetic field."
Albert
Einstein
|
Historical Sketch
James Clerk Maxwell was one of the greatest scientists and
mathematicians of the 19th century. With talents rarely united
today, he made landmark
contributions to both theoretical and experimental science.
Maxwell published phenomenal work in two areas. First, building
upon the experimental data of Michael
Faraday, and applying highly sophisticated mathematical methods,
he predicted the existence of electromagnetic waves (1864).
Moreover, he calculated the waves would travel at the speed of
light.
Later, Heinrich Hertz discovered these waves (1887) thereby
paving the way for radio, television, radar, and even the boom in
electrical
and
computer science. For Maxwell, the great mental
breakthrough came in thinking of electricity as an electromagnetic
phenomenon and
not some sort of mechanical process.
|
"The true logic of
this world is in the calculus of probabilites."
James Clerk Maxwell
|
Maxwell's other spectacular contribution was in the dynamical theory of
gases. His first great paper in the field was published in
1859. Today this subject is part of thermodynamics.
Josiah
Willard Gibbs, on the other side of the Atlantic at Yale University,
would join Maxwell in opening the door for exploration of the
physical and chemical properties of gases and other states of matter.
As is evident by his place of birth, Maxwell was the son of prosperous
parents. He was educated across town at the University of
Edinburgh, entering at the age of 16, and then Trinity College,
Cambridge. Eventually he became Cambridge University's first
teacher of experimental physics. He left retirement to serve as
the founding director of the Cavendish Laboratory of Cambridge
University.
He is buried with his family in the church yard of
Parton Kirk, Galloway, Scotland. |
|
|
|
 The house
where Maxwell was born is in a nice neighborhood near a park close to
the center of Edinburgh. The house now serves as a meeting place
for mathematicians and scientists and is home of the Foundation.
|
|
Feynman on Maxwell's Contributions
"Perhaps
the most dramatic moment in the development of physics during the 19th
century occurred to J. C. Maxwell one day in the 1860's, when he
combined the laws of electricity and magnetism with the laws of the
behavior of light. As a result, the properites of light were partly
unravelled -- that old and subtle stuff that is so important and
mysterious that it was felt necessary to arrange a special creation for
it when writing Genesis. Maxwell could say, when he was finished
with
his discovery, 'Let there be electricity and magnetism, and there
is
light!' "
Richard
Feynman in The Feynman
Lectures on Physics, vol.
1, 28-1. |
|
Purpose
of the JCM Foundation at 14 India Street . . . .
"To promote, encourage, and advance the study of, research into, and
the dissemination of knowledge of and relating to physics, chemistry
and physical chemistry in all their aspects and in particular, but
without prejudice to the foregoing generality, colloids and interfaces."
|
|
Scotland has honored Maxwell
in a number of significant ways . . .
|
and at Yale
|
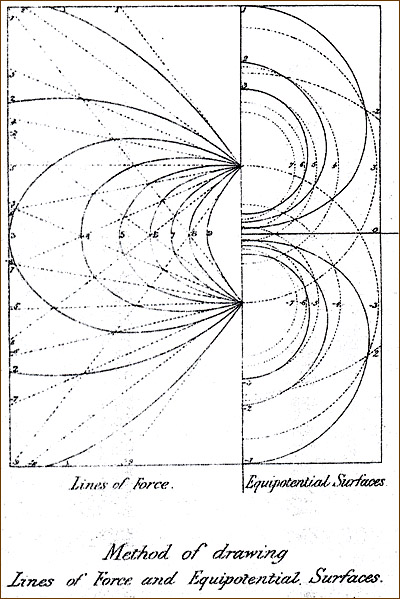
Maxwell himself on how to visualize a
single center of electrified force . . . .
"I am anxious that these diagrams should
be studied as illustrations of the language of Faraday in speaking of
'lines of force,' the 'forces of an electrified body,' etc. . . .
Now the quantity of electricity in a body is measured, according to
Faraday's ideas, by the number
of lines of force, or rather of induction, which proceed from it.
These lines of force must all terminate somewhere, either on bodies in
the neighborhood, or on the walls and roof of the room, or on the
earth, or on the heavenly bodies, and wherever they terminate there is
a quantity of electricity exactly equal and opposite to that on the
part of the body from which they proceeded. By examining the
diagrams this will be seen to be the case.
These diagrams are constructed in the following
manner:- First, take the case of a single centre of
force, a small electrified body with a charge E. The potential at a
distance r
is V = (E/r); hence, if we make
r = (E/V), we shall find r, the radius of the sphere for
which the potential is V
.
If we now give to V the
values 1, 2, 3, etc., and draw the corresponding spheres, we shall
obtain a series of equipotential surfaces, the potentials corresponding
to which are measured by the natural numbers. The sections of
these spheres by a plane passing through their common centre will be
circles, which we may mark with the number denoting the potential of
each. These are indicated by the dotted circles on the right
hand."
from
James Clerk Maxwell, "An elementary treatise on electricity,"
Clarendon
Press, 1881.
All readers
of this material will join the National
Curve
Bank - A MATH Archive in thanking the Huntington Library, San
Marino, CA, for permitting us to enjoy Maxwell's explanation and
illustration.
|
 |
|
Maxwell's
Four Equations
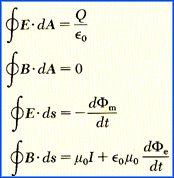
assuming there is no
dielectrical
or magnetic material (free space).
Note #4 is the same equation as
on the San Marino stamp.
|
|
Hertz on the left with Maxwell
on the right.
|
 |
For a
biography:
|
|
|
|
|
