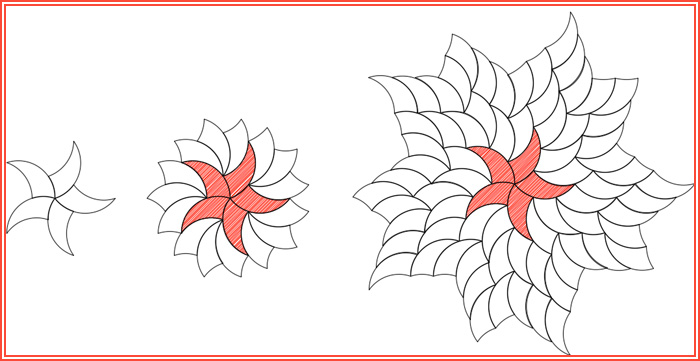
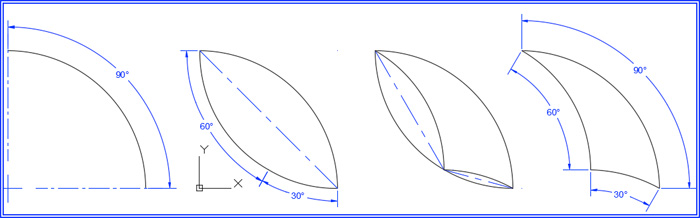
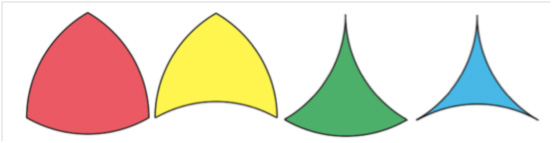
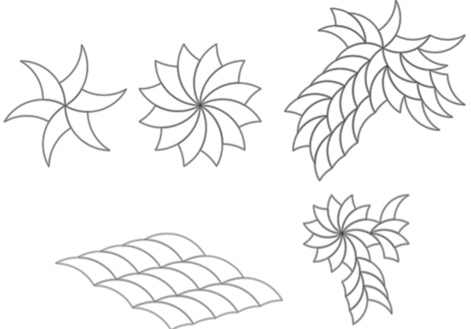
Click here for the full article.
|
|
|
|
[1] Bourke, P., Tiling with Tricurves (2017). < http://paulbourke.net/geometry/tricurves>
|
|
| Other spiral Deposits in the NCB: < ..//spiral/spiral.htm > < ..//log/log.htm > |
 |
 2018
2018 |