| Back to . . . .
 Curve Bank Home Curve Bank Home
NCB
Deposit # 101
Dr. Thomas Zettler
Munich, Germany
thomas.zettler@arcor.de
|

2-D and 3-D
Animations
The Tunnel Effect
|

All animations were created using
the Grapher
program in MacOS X.
|
| The
"Tunnel Effect" has a wide range of consequences and applications in
daily life. For example, the storage of photos in digital camera
storage cards and the modern scanning tunneling microscope
both depend
on a tunnel effect. |
Two animations . . . .
Equations
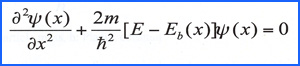
The Tunnel
Effect is based on complex valued wave functions where a solution
begins with the one-dimensional stationary Schrödinger
Equation as seen above. Dr. Zettler has provided readers of this
NCB web page with a detailed explanation in a "pdf" file. Be sure
to give him credit if you use his material.
|
| References |
M. Alonso and
E. J. Finn, Fundamental University
Physics, Volume III, Addison-Wesley, Twelth Printing
1980, LOC Catalog Card No. 68-10828.
|
W. C. Elmore
and M. A. Heald, Physics of
Waves, Dover Publications, 1985.
|
L. D. Landau
and E. M. Lifschitz, Lehrbuch de
theoretischen Physik, Band III
Quantenmechanik 6, Auflage, Akademia Verlag Berlin.
ISBN-10: 3055000676 and ISBN-13: 978-3055000676
|
A. Messiah, Quantenmechanik, Band 1, de
Gruyter, Berlin, 1976.
ISBN 3-11-003686-X. (German translation
of a French book, Mecanique
Quantique Tome 1, by Dunod, Editeur , Paris 1969.)
|
|
|
|

|
 6/26/2010
6/26/2010
|
|