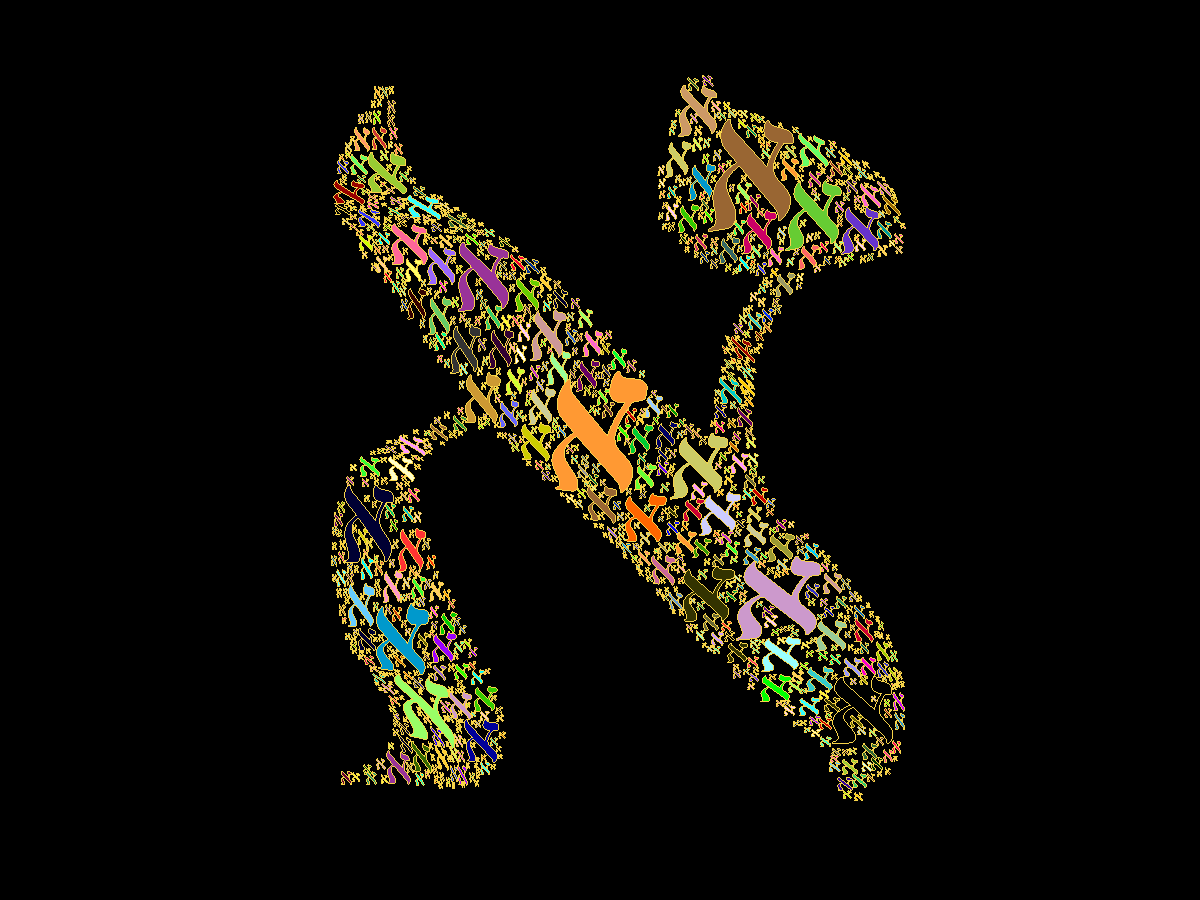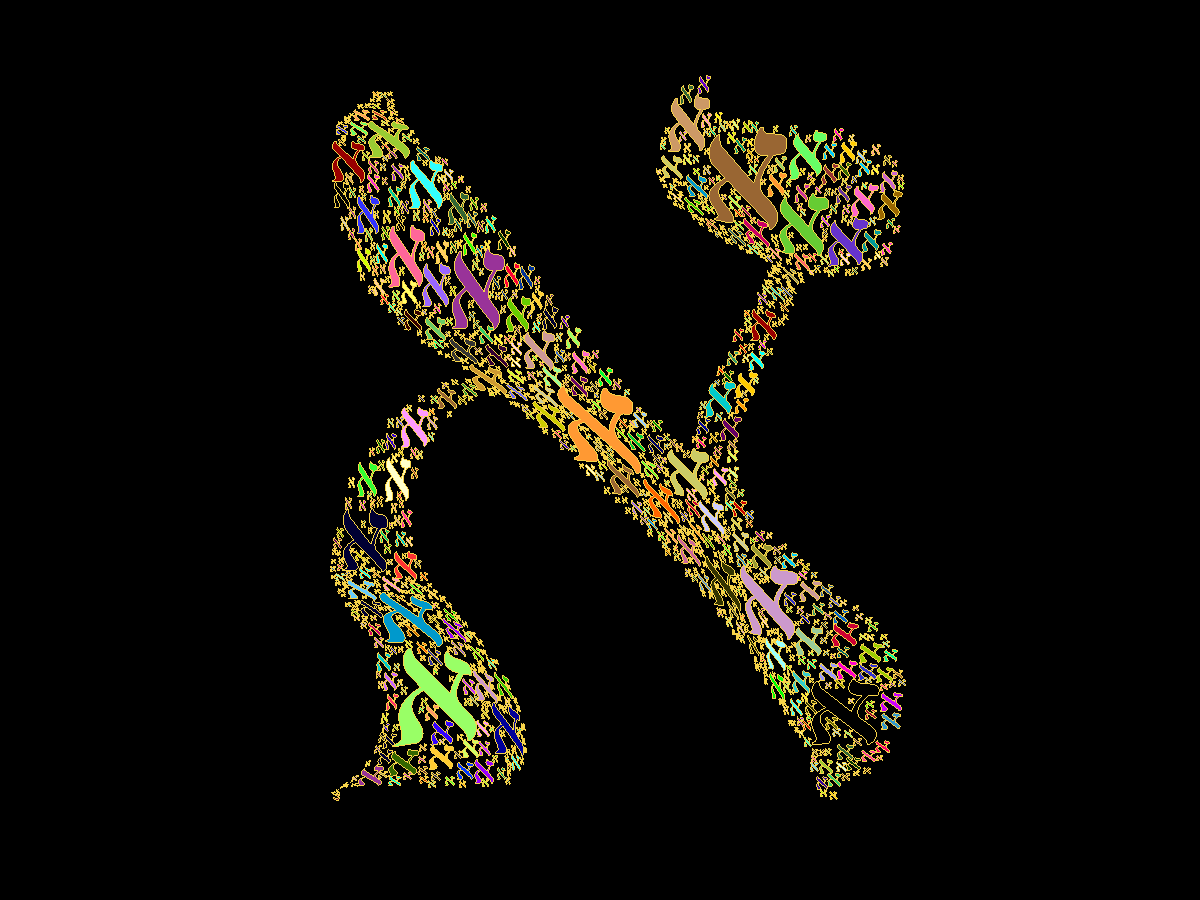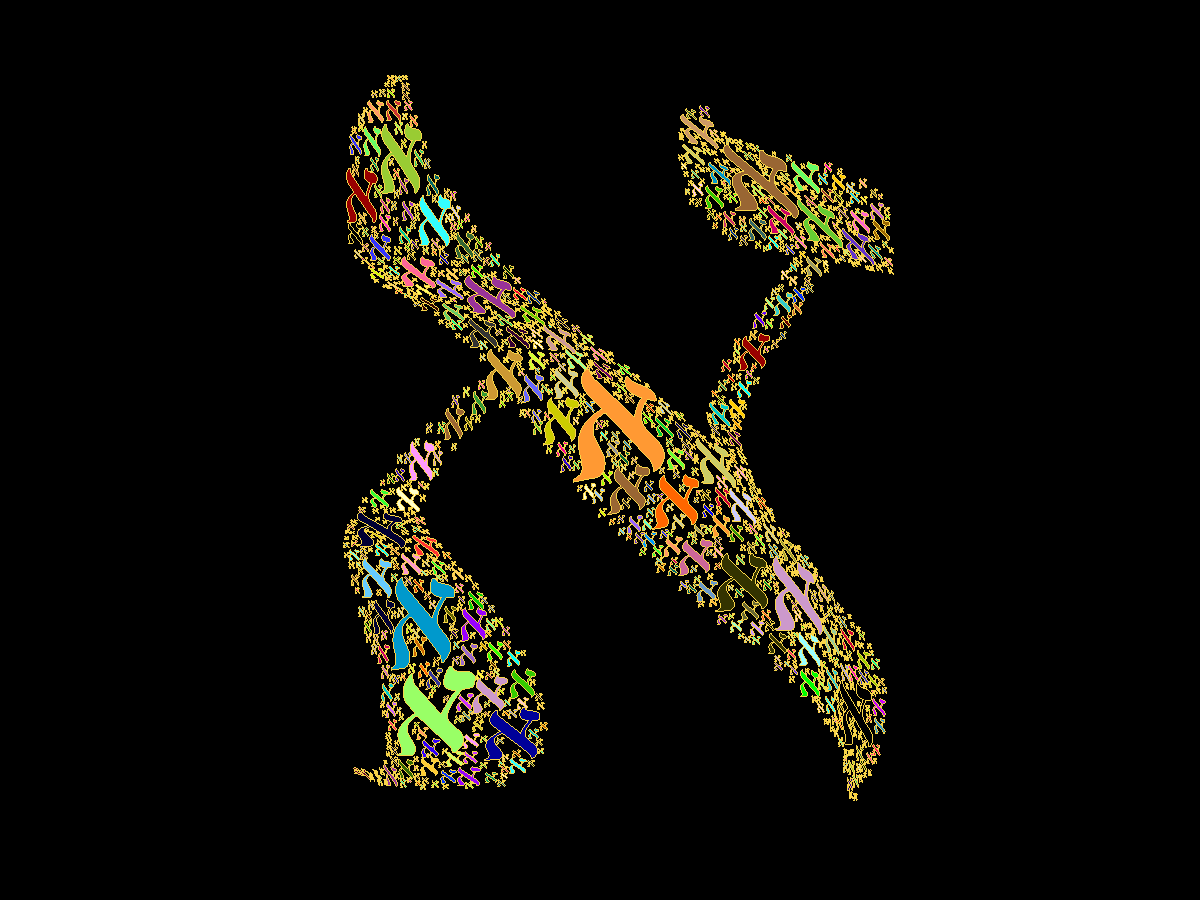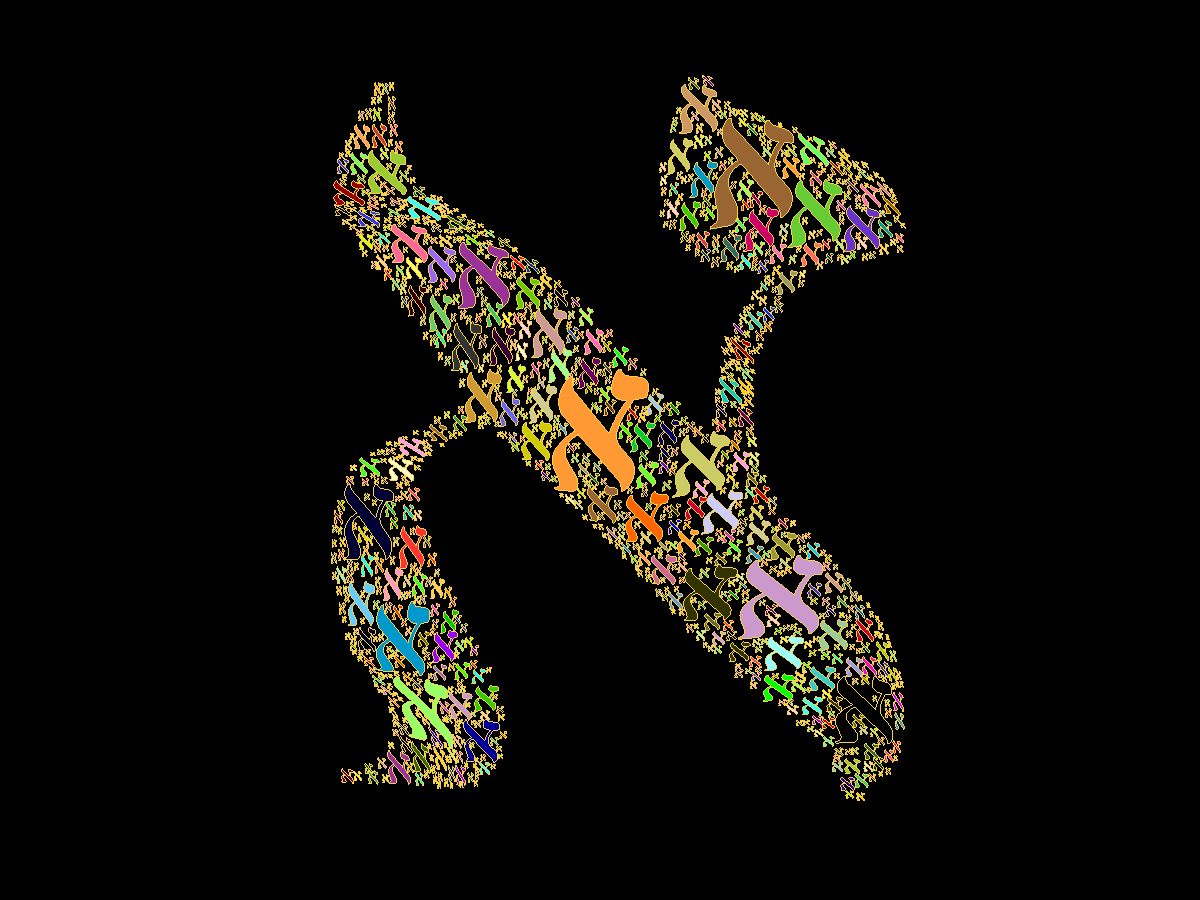Aleph Animation

Back to . . . .

Curve Bank Home
Curve Bank Index

NCB Deposit # 141

Dr. Cye Waldman
cye@att.net

A Mathematician's Delight . . . .

The Paradox of Greater and Lesser Infinities

Waldman has developed an ALEPH that propagates to fill an "aleph." In mathematics, the aleph is now universally accepted to represent countable and uncountable sets. The symbol was selected by Georg Cantor from the first letter of the Hebrew alphabet. His work sparked one of the greatest discussions in late nineteenth century philosophy. This led to the "New Math" and evolution of set theory abounding in 1960-70s.

However, the inspiration for this particular work came later and is attributed to John Shier. In 2010, Shier introduced the concept of statistical geometry and addressed the question,

"How do you cover a bounded region non-recursively with an infinite number of ever-smaller randomly placed simple shapes such that in the limit they completely fill it?"

John Shier

We say that the shape is 'fractalized,' such that the size distribution of the objects appears to be self-similar at all scales.
See < http://john-art.com > .

"This image was created using a statistical geometry program developed by the author. It was then altered by a sinusoidal transformation of the absolute value in the complex plane, originating at the lower left. The animation was created by variation of the phase angle. We call this a Vasarely transform, in recognition of the great op-artist Victor Vasarely, of the mid-to-late 20th century. The animations below demonstrate radial and azimuthal Vasarely transforms."

Dr. Cye Waldman

Copyright Notice: This animation and all images within are under copyright by Cye Waldman and may not be copied, electronically or otherwise, without his espress permission.
Dr. Cye Waldman
cye@att.net

References

An Award Winning Biography:

Joseph Warren Dauben, Georg Cantor, Princeton Univesity Press, 1990.

"Dauben's study is the "most thorough yet written of the philosopher and mathematician who was once called a 'corrupter of youth' " for the New Math being introduced into elementary schools.

A Less Formal Explanation for Non-mathematicians:
< http://www.coopertoons.com/education/diagonal/diagonalargument.html >

Other Waldman contributions to the NCB:
Sinusoidal Spirals: < ..//waldman/waldman.htm >
Bessel Functions    < ..//waldman2/waldman2.htm >
Gamma Funcions   < ..//waldman3/waldman3.htm >
Polynomial Spirals and Beyond   < ..//waldman4/waldman4.htm >
Fibonacci and Binet Spirals with a touch of Mondrian < ..//waldman6/waldman6.htm >
"Other" Fibonacci Spirals and Binet Spirals < ..//waldman7/waldman7.htm >
< ..//waldman8/waldman8.htm >
< ..//waldman9/waldman9.htm >
< ..//waldman10/waldman10.htm >

The NCB thanks Dr. Waldman for his strong contibutions.