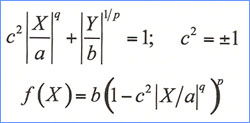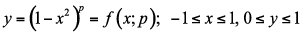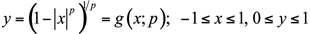|
In
MATLAB . . . . . . .

Superconics
Animation
Code
|
|
Why Superconics?
Cye H. Waldman
There is a plethora of super this-and-that running around the
mathematical world these days: superellipse (and its 3D cousin,
superquadrics), supercircle, superparabola, superhyperbola, and
superformula. So why do we need superconics?
Superconics is a system of curves, based on the conic sections, for two
and three-dimensional shapes. With the exception of the superformula,
all of the above are subsets of superconics. In one equation,
superconics describes all of these and more. Moreover, it is amenable
to exact mathematical analysis. Specifically, a single analytic
solution gives the area, centroid, moments, and volume of bodies of
revolution over the wide range of variables embraced by superconics.
Superconics provides a systematic set of functions for evaluation of
various problems. This has allowed us to extract certain mathematical
relations that may have gone unnoticed heretofore.
Superconics is essentially a two-parameter function, with one
additional switch that distinguishes elliptic/parabolic and hyperbolic
types. Extended superconics is a three-parameter function that provides
the full spectrum of curves between and beyond elliptic and hyperbolic
types. This function completely blurs the distinction between the two
types; you can transition smoothly between them. The extended
superconics likewise has a completely analytic solution.
As for the superformula, it’s merely an elaborate curve-fitting
equation with four parameters in addition to axial scaling, cleverly
guised in mathematical notation. There are no mathematical properties,
per se, because it’s intractable. Its properties can only be determined
by direct numerical simulation; but then it’s doubtful that any of its
acolytes has ever looked.
In our studies of superconics we have come to develop new
understandings that can be readily ported to other areas of interest.
In the mathematical arena, we have demonstrated new relations between
volume and centroid and the plane curves that generate them.
In our studies of superconics in three dimensions, we have developed an
algorithm for 3D shapes that allow
the generating curve (or vertical
profile) to vary continuously while tracing out the base curve.
And that is why superconics.
|
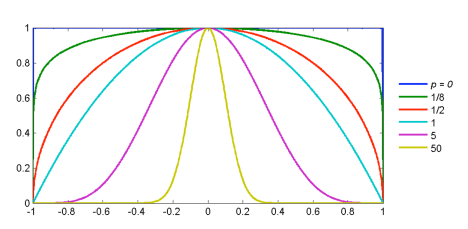
Superparabola
A sampler of curves in the superparabola family. Note the pulse for large values of p.
We define superparabola as a parabola
raised to a positive power
greater than or equal to zero. Example:
|
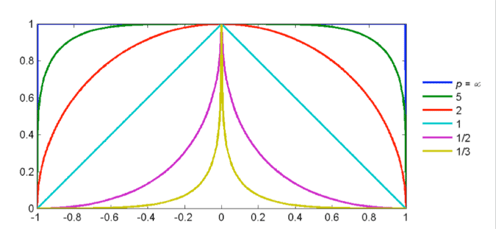
Superellipse
 A
sampler of
curves in the
superellipse family. Note the cusp for small values of p.
A
sampler of
curves in the
superellipse family. Note the cusp for small values of p.
The superellipse, also known as the Lamé curve, is used in the
following form for the cylinder footprint:
|
|
Superconics:
Hyperspheroid

and the equations .
. . . .
|
Another Version of a Superconics Hyperspheroid

|
|
Methods: Writing the Program
All 3D figures and
animations were created with a program developed by the authors. The
crux of the program is the spherical product routine that is
essentially the product of a matrix and a diagonal matrix. The input
parameters are an n-by-n matrix (n-by-n column vectors for the vertical
ribs) and an n-vector (the planiform curve). These are as
expressed complex variables; in the matrix, the real and imaginary
parts are the radial and vertical components of the vertical ribs,
respectively.
In the main
program, the n-by-n matrix is calculated sequentially around the
planiform based on the local vertical profile. All the vertical
profiles are superconics, but the need not be. Toroids and Mobioids can
be created with a few control parameter settings. And the same program
applies to the extended superconics with 3 parameters or complex
parameters.
We have used the
same program to create 3D forms from regular and star polygons, cuspids
and rosettes, Reuleaux triangles, superformulas, and more, even
fractals (imagine a Koch snowball created form Koch snowflake).
Moreover, any of these forms can be mixed and matched; the program does
not care.
In addition, we
have used the same program, albeit with some ad hoc modifications to
create twisted cylinders, the Archimedean hoof, sphericon, tractroid,
and more.
|
Copyright Notice:
The animations and all images within are under copyright by Cye Waldman
and may not be copied, electronically or otherise, without his express
permission.
Dr. Cye
Waldman, cye@att.net
|
|
|