|
TheThe NCB thanks members of our National
Advisory Board for
annually selecting the best
deposit of the previous year.
 |
2016
Deposit
#150
"Sphericons"
The National Curve
Bank honors
David Hirsch.
<> "Two Cones with a Twist".

Created in SolidWorks, saved as AVI and then
transformed to GIF
|

|
2015
Deposit
#147
"The
Method of Archimedes"
The National Curve
Bank honors
Cye Waldman, Gustavo Gordillo and Daniel Ye Ding
<> Propositions 13 and 14 of Archimedes
MATLAB and MATHEMATICA with 3-D Printer Models
Moreover, we found the Golden Ratio!
See Notices, October,
2016
|

|
2014
Deposit
#138
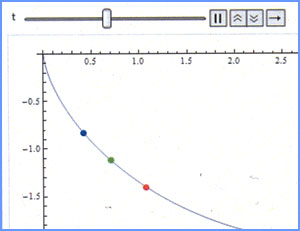
<> Tautochrone in
MATHEMATICA and its Wonderful Connection to American Literature.
Huygens, Newton, Jean Bernoulli,
Euler, Lagrange and Herman Melville,
among others, have all been captivated by the special properties of the
tautochrone.
"It was in the left hand try-pot of
the Pequod, with the soapstone diligently circling round me, that I was
first indirectly struck by the remarkable fact that in geometry all
bodies gliding along the cycloid, my soapstone for example, will
descend
from any point in precisely the same time."
from Moby Dick, 1851
|
 |
2013
Deposit
#127
<> Spirals in
Matlab: The Golden Ratio with Mondrian Shading.
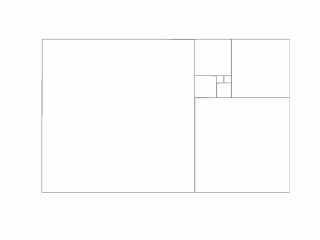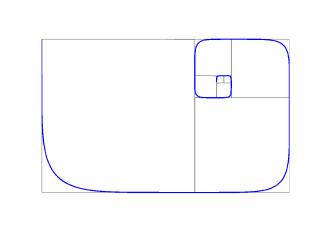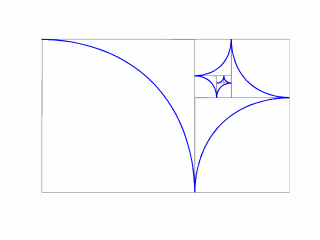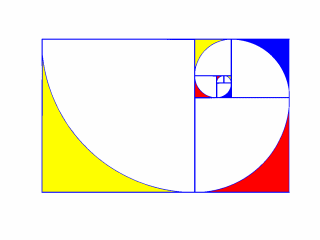
Waldman finds calculations with spirals to be amusing "because an
approximation should be easier than that which is being approximated."
|

|
2012
Deposit
#113
Fractal
Animation
The National Curve
Bank honors
Chaya Morasha Gilbert-McNabb.
<> Julia Sets in MATHEMATICA®.

Among the new notation introduced in Harriot's algebra book Artis Analyticae Praxis published
by his friends.
|

|
2011
Deposit
#111
Wooden
Models of the Conic Sections
The National Curve
Bank honors
Francisco Treceño of Valladolid, Spain.
Treceño is a master wood lathe
craftsman.

Following a National Curve Bank tradition of supporting craftsmen
producing models of mathematically related forms, we are honoring
Treceño for his video demonstrating the union of wooden conic
sections.
|

|
2010
Deposit
#103
The
Cannonball Curves of Thomas Harriot
The National Curve
Bank honors
Dr. Janet Beery, University of Redlands
and
Dr. Louis Talman of
Metropolitan State College, Denver.
Harriot investigated projectile
motion in the 1600s.

Among the new notation introduced in Harriot's algebra book Artis Analyticae Praxis published
by his friends in 1631, ten years after his death, were the symbols for
less than and greater than, < and >, that we use today.
|

|
2009
Deposit
#98
<> Quasi-Spherical
Orbits and Surfaces
The National Curve
Bank honors
the historic animations
created
by
Robert G. Chester,
Intellectual Properties Associates
Tumwater. WA
.
Leibniz collaborated with Bernoulli
to publish
a wonderful illustration of a quasi-spherical
orbit.
|

|
2008
Deposit #84
The
Catenary or "Chain" Curve
The National Curve
Bank honors the catenary
created by Dr.
Gary Brookfield of
California State University, Los Angeles.
"All five of the finalists this year
deserve to be winners. The hinged dissections (#89)
and the circle (#85)
are nice; and the catenary is a classic curve if there ever were one."
A
member of the National Advisory Board of the NCB.

From Schooten's Latin
edition of Descartes.
Be sure to note Descartes' axes were not always perpendicular.
|

|
2007
Deposit #81
How to
Visualize a Contour Map
The National Curve
Bank honors the contour maps
created by Dr.
Louis Talman of
Metropolitan State College, Denver.
"I'm teaching Calc 3 this term. My students are struggling
(as they always do) with visualizing things like this. I'm
showing this in class today!"
A
member of the National Advisory Board of the NCB.

From one of Descartes'
hallmark problems
investigating roots and
signs of polynomials.
Be sure to note the equals sign used by the printer was that of the
horoscope's Gemini.
|

|
2006
Deposit #64
Vector
Fields
In his work, Dr. Dray recognizes
the stellar contributions of
Hamilton,
Maxwell
and Gibbs.
He thus represents mathematics
from
Ireland, Scotland and the United States.
The
National Advisory Board of the NCB.
The National Curve
Bank honors the interactive vector fields
created by
Dr.Tevian Dray of
Oregon State University
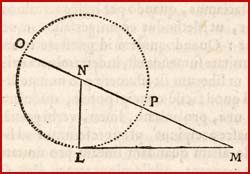
From one of Descartes'
hallmark problems
uniting algebra with
geometry.
|

|
2005
Deposit #58
The
Brachistochrone
"For the Shrewdest Mathematicians
of All the World"
Johann
(Jean or John) Bernoulli
June,
1696
The National Curve
Bank honors the animations
developed by
Gustavo Gordillo of
Verdugo Hills High School
Los Angeles Unified School District
|
|